一个很难看出破绽的永动机设计
在《费恩曼物理学讲义 第一卷》第46章中有一个尝试违反热力学第二定律的永动机设计,乍一看貌似还真能实现,我当年就怎么也看不出来这个装置哪里出了问题,最近终于是明白一些了,就写在这里给大家看看吧。
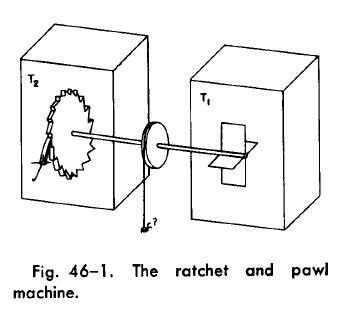
直接用热力学第二定律就可以否定这个装置成功的可能性,但是如果不从力学以及热力学的其他基本定律对该装置予以反驳的话,我始终觉得难以令人信服。那么,到底这套装置哪里出了问题呢?为什么这样的装置不能达到他永动机的目的?
在看我的分析之前,你最好自己仔细思考思考。
我们必须更仔细的研究装置的细节。这个装置给人最初的印象是能做成永动机,主要是因为细节还没有丰富到让你看出破绽。我们对棘轮必须加以理想化,但是,总还得有个掣爪,而掣爪上又必须有一根弹簧。这一特征没有在图上画出来,但却是很本质的特征。轴想要顺时针转动(从右往左看),为了把掣爪提高一个轮齿的高度,必须克服弹簧弹力做功,我们设这个能量为ε。系统凭借气体无规则运动的涨落可以积聚起足够多的能量ε的几率是e^-(ε/(kT))。但掣爪由于偶然原因而提高的几率也正好是e^-(ε/(kT))。这两个几率是相等的,因此那个可怜的小臭虫只会不停的上下晃动而不会如原来想象的那样一直上升。平常生活中我们是从来没有考虑掣爪由于偶然原因而提高这一事实的,因为这个概率实在是小得我不忽略它都对不起它,我们主动操纵棘轮时可以放心的让他单方向转而不出现意外。而现在棘轮的驱动力也是一个小之又小的力,掣爪的偶然提升已经和这件事发生的概率同数量级了。
如果想看对这个问题更加深入和详细的分析,请看《费恩曼物理学讲义》。
连这么完美的永动机设计都被挑出毛病来了,可见热力学第二定律的正确性的确不容置疑!



牛
问个问题 假如光波的波长增加到和声波一样 也就是说光波的衍射变得非常明显 我们将会看到什么? [email protected]
会看到一些条纹,高中课本上就有图片
好后悔买了英文版的……
呵呵,我也买了英文版啊,用来学英语或者收藏都不错。不过如果没有中文版的看起来是挺费劲的
如果将棘轮和掣爪换成一个很小的理想的发电机,能否产生交流电,并把热能转化成电能呢?
应该是可以的,但是这么小的交流电,在使用的时候就相当于是白噪声了。如果想要定向的做功还需要个二极管。同样的问题,e^-(ε/(kT))使得二极管没法使这个电流变成有效的能量,还是无规则的能量,和热运动没区别
热二……让我想起一篇经典的科幻小说,the Last Question.
如果气体无规则运动的涨落积聚的能量大于ε,你的解释还成立吗?
还有“zhanjian ”的回复,也可以形成一个能量不守恒的突破口?
你如何解释???
这个模型应该是能量守恒的,但不应该是你这样的解释。
如果这个模型是在真空中,和外界没有能量交换,里面空气分子的速度应该是越来越慢,空气的温度越来越低。
这才是这个模型合理的解释。
我刚才温习了一下热力学第二定律,这个模型有个矛盾。
热力学第二定律只能适用于由很大数目分子所构成的系统及有限范围内的宏观过程,如果从宏观角度看的话,模型根本就不会转动,可怜的小虫,只会一动不动。如果从微观角度看的话,比如里面只有少量气体分子,小虫会一直被提升(根据我上面的解释)。
但是,这就不是热力学第二定律的范畴了。
一个比棘轮和掣爪更难看出破绽的永动机设计
http://bbs.sciencenet.cn/showtopic-97614.aspx
我想说:靠,高中时候我设计过一个类似的。
后来没学物理,淡忘了。今儿稀里糊涂进了你的博客。
我当时的设计中,没有采用棘轮,而是使用压电陶瓷。把分子的每次撞击转变成电能先,有可能吗?
【思考】2,系统A、B,A的温度低于B。利用光电效应,能否从A中产生电能,传输到B中,继续提高B的温度?假设A中的温度高到足以产生光电效应——或者别的能从光转化成电能的效应。(我没有阐明的条件都当作理想条件)
【思考】3,如果普通状态下热力学第二定律牢不可破的话,与恒星、黑洞、大爆炸联系起来是否仍然也是牢不可破的呢?
比如说两大团气体A、B,A中的温度低于B,形成了恒星,最后塌缩成黑洞,然后再有一大堆乱七八糟的变化,再次成为两大团气体。有没有可能产生A向B输送能量的结果?
【思考】4,宇宙热寂之后,会不会由于重力作用使恒星再次点燃,熵减少?
另外,9L的链接打不开。
看了前面的回帖,觉得都不太合理。楼上的“上帝之手”又太抽象了。想了一下具体化的描述。我们就把“上帝之手”当成一个有形的棘爪。这个棘爪要敏感到控制到一个分子碰撞,那么棘爪也应该是分子尺度的,所以这个棘爪将不能看作我们通常所认为的简单刚体。也许可以这样假设,维系这个分子尺度棘爪的功能发挥作用,必定需要投入某一定能量,来保证其分子键不发生扭曲或断裂。这样的能量投入也就与本身机器所产生的能量相抵消。所以能依然维系第二定律的成立。
嗯,气体分子对叶片做功后能量减少,运动减慢,如果此时转动的叶片又对气体分子做功,气体分子恢复原有能量,似乎又可以重复上面的过程了,看起来似乎可以永远转动。但是问题来了,叶片对气体分子做功后叶片的能量与状态如何变化?对气体分子的运动有什么影响?