一个电磁学“佯谬”
高中时候看到《费恩曼物理学讲义》第二卷17-4《一个佯谬》的时候,非常困惑,如今终于明白了一些,虽然具体的计算工作还做不了。这个佯谬是这样的: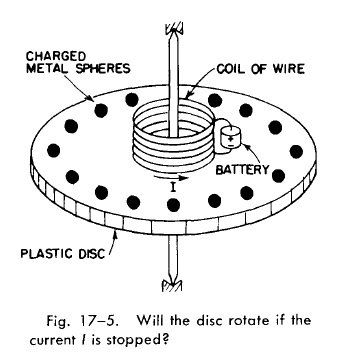
试想构造一个如右图所示的装置。一个绝缘的圆盘通过摩擦力可以完全忽略的轴承套在一个轴上,可以自由旋转。圆盘上,放着一个与之同轴的线圈,通过这个线圈的电流由同样是放在圆盘上的一个小电池提供。圆盘的边缘上固定着一些金属球,注意它们是和圆盘固连在一起的,这些小球每一个都带有一定的电量Q。现在初始条件为有电流通过,整个装置静止不动。
现设想,如果突然切断电源旁的一根导线导致电流变为0,整个圆盘会发生转动吗?电流减小,导致通过线圈的磁通量减少,而磁通量的变化会在空间中激发出感生电场,感生电场的方向为圆形,可以使全部带电的金属球受到圆盘边缘切向方向的力,从而产生一个净力矩导致整个圆盘转起来。然而,从另一个角度来分析,将得出截然相反的结论:因为切断电源的力大小可以忽略,对整个系统没有力矩的贡献,所以整个系统角动量守恒,圆盘仍然将保持不动(整个系统包括圆盘、金属球、线圈以及电源)!
为什么两种途径的分析会产生截然不同的结果呢?真实的物理情景到底是转还是不转呢?
高中时的我曾以为是要考虑线圈里电子的运动从而使得系统一开始就具有不为零的角动量,其实这显然是错误的,很容易发现其中的破绽,倘若使金属球带相反的电荷,整个圆盘最终将朝着另一个方向旋转,但是初始角动量还是原来的方向,所以明显不对。那究竟是怎么回事呢?
真正的原因是,电磁场具有角动量!高中时的我正是因为没有明白这件事情,所以才一直没有想通。初始状态时,有电流,因此空间中有电磁场,这电磁场就具有一定的角动量,末状态时电磁场消失,电磁场的角动量全部转化为机械角动量,因此圆盘旋转,角动量亦守恒。至此矛盾自然消失。我们刚刚学了一点点磁矢势的概念,因此对电磁场动量加深了理解,但是对于电磁场角动量如何计算还没有太深的研究,因此对上述分析也只能止步于定性分析了。
很显然,像角动量守恒这种原理是永远也不可能被打破的。一旦发现在某种物理过程中角动量似乎不守恒了,要做的事情非常简单,只要在原来的角动量表达式里面再加上一项新的项就可以了,总可以保证有某个角动量量纲的东西继续守恒,我们仍然称之为角动量即可。



看到第二卷十七章了,我要努力加油了。
从感生电场的方面考虑,最后体系的机械角动量显然与载流子所带电荷量无关。 然而从总角动量守恒的角度来看,则应该同时考虑载流子携带的角动量和电磁角动量。 这样,两种理解似乎有点不同。 哪里有问题?
电磁角动量…其实这个模型处理电磁角动量时候还是有一点问题的,比如说你假定螺线管无限长,你能算出一个总角动量不守恒…