最小作用量原理与物理之美5——对称守恒与作用量
作用量的形式变幻多端,有人曾问过我我们是怎么知道作用量的表达式的。我想说的是,人类还没有一套完整的直接写出不同领域的作用量的方法,但是利用物理定律的对称性人们可以更容易得找到正确的作用量。物理定律的对称性和平常所说的几何对称还稍有不同,我来简单介绍一下吧。
对称的定义要点是这样的:如果有一样东西,我们可以对它做某种事情,在做完之后,这个东西看起来依旧和先前一样,那它就是对称的(见《费恩曼物理学讲义 第一卷》第52章)。比如我们熟悉的轴对称图形,我们把它经过镜面反射,它看起来和原来一样,因此它就是对称的。
作用量的对称性就是物理定律的对称性。对于物理定律来说,他们应该满足一些对称性。例如,F=ma这样的定律,我们在实验室做实验、在海底做实验、在外太空作实验都可以得到,不会在哪里发现F=2ma或者F=m^2*a。我们称这些物理定律满足空间平移对称。物理定律还满足时间平移对称,我们一百年以前做的实验发现的定律,现在再做还会发现同样的定律,一百年以后依然如此,物理定律的形式不随时间的流逝而改变,就称这些定律满足时间平移对称。还有一个比较普遍的对称称为空间旋转对称,即我们无论脸朝着哪个方向看到的物理定律都应该都是相同的。以上三个对称性,是适用于所有物理定律的,至今没有发现任何物理定律例外。…
最小作用量原理与物理之美0——导言
爱因斯坦说过:“我想知道上帝是如何设计这个世界的。对这个或那个现象、这个或那个元素的谱我不感兴趣。我想知道的是他的思想,其他的都只是细节问题。”近代物理隐隐约约的表明,我们人类似乎已经接近于上帝的终极设计了,最小作用量原理、对称与守恒可能就是上帝设计世界的原则。最小作用量原理、对称与守恒不同于F=ma、F=GMm/r^2、F=kx、F=kQq/r^2这类的普通物理定律,他是物理定律的定律,是一切其他普通物理定律的基础。
最小作用量原理是一个令人神往的课题,费恩曼上高中时听到他的老师巴德给他讲的时候就被深深震撼了,我也是一样。当我第一次从费恩曼的书中看到这个原理时,真是有种无法言表的喜悦,好像是我窥见了上帝设计世界的图纸一般。后来我就如饥似渴的学习者有关引人入胜的最小作用量原理的知识,同时越来越被这伟大的原理所吸引。…
机械能守恒需要特殊参考系么?
一个从静止(相对于地面静止,将地面称作S系)开始自由落体的物体满足机械能守恒这是大家闭着眼睛都知道的事情,可是一天我突然想到了一个问题。如果我们换一个参考系,假如说我乘坐着一个电梯,以10m/s的速度(相对于大地)匀速下降,以我为参考系(称作S’系)来看前面这个自由落体的物体,机械能还守恒么?考虑到1秒的时候,物体相对于地面的速度也恰好是10m/s,我们不妨以0到1秒这段时间的状态来研究。一开始0秒的时候,物体相对我(S’系)有10m/s的向上的速度,势能是mgh。在1s钟这个时刻,相对于S’系物体静止了,即动能为零,而高度减小了,即势能也减小了,这样看来机械能不就不守恒了?!
这可能么?一个物理过程,以地球为参考系,机械能就守恒,而换一个相对它匀速运动的新参考系,机械能却不守恒了?强烈的物理思想告诉我,宇宙中不存在特殊参考系,能量守恒在任一惯性系中都一定是成立的。既然地球近似的看成惯性系机械能守恒了,那S’系没有任何理由违反机械能守恒!
问题出在哪里呢?对这个问题,我苦苦思索了两天,终于在一天睡觉的时候悟出来了。原来,问题就出在地球这个“近似”的惯性系上。虽然地球质量极大,在处理一般问题的时候可以认为是很好的惯性系,可是就在现在这个小问题上这个近似出现问题了。请听我慢慢讲解。…
高考物理教育的失败——一个经典模型之错误
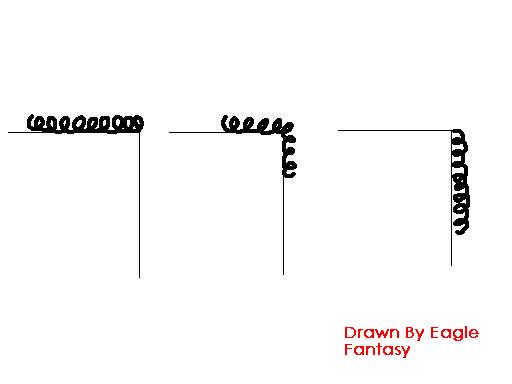
想必学过机械能守恒的高中生都作过这么一类题吧,如图,一个铁链原来静止的放在水平面上,漏出一点点可忽略不计,然后他会在重力作用下下滑,告诉你铁链的质量、长度一类东西,问你完全离开平面式铁链的速度(图中第三个状态)。
我当时也作过这一类题,《中学第二教材》把它当作一个重要专题来讲,训练机械能守恒。甚至在程稼夫《力学篇》上,都有一道类似的题,只不过麻烦一点就是了。
浙大讲动量能量的老师出出来这道题之后,我都很惊,这么简单的题,做个包子?一个机械能守恒不就完事了么。令我没有想到的是,经老师一点破,发现这道题是倒错题,所有这种类型的题全错了!…
用逻辑学规范物理学(三)
也许我是受费曼的熏陶太深,也许我就是思想顽固保守,我总相信宇宙有一套自然公理,而通过这套公里就可以完全用逻辑学的推理,把所有宇宙定律全部推出来。我知道这个问题不是我现在所能研究的了的,但我还是太狂热。那么,就让我冒昧的先把最基础的牛顿时代的定律加以整理吧。
至于自然界的公理是什么,我还是要说我受费曼的影响太深。费曼认为,宇宙中最基本的两个原理应该是对称守恒和最小作用量原理。我深表同意。这两个原理,我自认为无可厚非的成为宇宙中的最基本公理。关于对称守恒的原理,我还是想选择Noether定理(诺特尔定理)作为基本公理,该定律内容是这样的:宇宙中对称与守恒是一一对应的(它们之间有着某种妙不可言的神秘关系)。例如:空间平移对称对应着动量守恒,时间平移对称对应着动量守恒,空间方向对称对应着角动量守恒,规范性变换对称对应着电荷量守恒,左右对称对应着宇称守恒(这组守恒似乎是破缺了),等等。
有了这组公理,我现在开始推。
首先,考察一些事物的属性。作为空间,他有几个固有性质:平移对称,各向同性,连续性,无限性,有三维(比较保守的观念)等。(引用自:《科学与假设》,彭加勒著)作为时间,他也应该有几个固有性质:平移对称,反演对称(似乎是部分破缺的)等。在关于时间的问题上,我不敢多讨论,也不想多讨论,因为连最牛的科学家都说不清道不明。
因此,通过Noether定理,我就得出了以下几条定理:…
几本很好很强的物理书
最近一个学期,每星期必去一次书城,每次去都有买几本书的冲动,除非没带钱。虽然大部分书闲置了,但真有一些好书值得反复品读。
《可怕的对称》(阿·热 著)这是一本很出名的物理学科普书籍,我看了许多的科普书的引用里面都有它,甚至连机械工业出版社出版的《大学物理》教材都要引用它。里面讲的对称思想,至今使我激动不已,原来是世界是这么美妙。
《物理定律的本性》(R·P·费曼 著)名字里有”RP”,人品就是高啊!这是一位获得过诺贝尔奖的物理学家,在量子电动力学有卓越的贡献。而它又是一位天才似的科普演讲家,他在康奈尔大学的演讲,也就是这本书的出处,取得了巨大成功。他用的都是最先进最有趣的物理思想、最生动最易懂最贴切的比喻、最平易惊人的语言,用几乎小学生水平的数学,讲述了物理定律的本性,我看得十分着迷。
《自然哲学之数学原理》(艾萨克·牛顿 著)这本书最强,不用说大家应该也知道,这是物理大厦的奠基之书,被誉为世界上最伟大的科学书籍。这本书挺难(对于我这种低智商的人来说),因为牛顿在这本书里已经大量使用它自己发明的现在被称为微积分的数学工具了。里面讲了力学、运动学、流体力学、天文学、潮汐等有关定理。
原来物理世界这么神奇,居然有着对称、守恒、最小作用量原理这样的普适原理,在人类目前可以达到的范围内放之四海而皆准!!!无论是牛顿力学还是麦克斯伟电磁学,无论是相对论还是量子力学,都离不开他们的身影。。。神奇啊啊!!!…


