相位同步与藏本模型 (Phase Synchronization and Kuramoto Model) 的形象展示
在读PhD的时候,有一门课讲到了相位同步 Phase Synchronization 的现象(藏本模型 Kuramoto Model),当时学的似懂非懂。今天偶然看到了一个实验视频(原地址是 https://www.youtube.com/watch?v=Aaxw4zbULMs,在墙外),直观的展示了相位同步现象。鉴于这方面的中文资料非常少,就发布一下这篇文章喂给搜索引擎吧,希望以后大家用中文搜索相关内容的时候也能看得到这个直观的视频。
相位同步现象属于我比较感兴趣的那类现象:设定非常简单,就是简谐振动+弱耦合而已,完全属于经典力学的范畴内一点玄学都没有,但是却可以产生非常 non-trivial、反直觉的结果。还有一个类似的例子是倒立单摆的稳定性与 ponderomotive force。
至于为什么这个简单的实验装置是藏本模型 Kuramoto Model 的一个具体实现,见这篇文章:
至于为什么藏本模型 Kuramoto Model 是一个很普遍的模型,在很多完全不同的物理系统中都可以出现,感兴趣的话可以阅读更多资料,例如:
…如何计算湍流能谱
最近在如何数值上计算湍流能谱(turbulent energy spectrum)上面卡了好几天,现在终于问到了做过的人看了相应的书明白了正确的算法。写出来以供自己留个记录以及给搜索引擎喂食吧。
问题定义:现在已知速度场\(\mathbf{u}(\mathbf{x})\),求能谱\(E_k(k)\)。(我研究的问题是2D的,所以以下都按照2D来写了,推广到3D也是非常容易的事情。)
能谱的含义是动能在k空间上的分布函数,其对k进行积分之后将得到总的动能。其定义为:\[E_k(k)=\int\frac{1}{2}\Phi_{ii}(\mathbf{k})\delta(|\mathbf{k}|-k)d\mathbf{k}\]
其中\(\Phi_{ii}=Tr(\Phi_{ij})\)(其中ij取12,如果是3D情况则ij取123)
其中\(\Phi_{ij}\)为关联函数(correlation function)的傅里叶变换:\[\Phi_{ij}(\mathbf{k})=F\{R_{ij}(\mathbf{r})\}\]
其中\(F\{.\}\)是傅里叶变换的记号,而\(R_{ij}\)为关联函数:\[R_{ij}(\mathbf{r})=\langle u_i(\mathbf{x})u_j(\mathbf{x}+\mathbf{r})\rangle\]
其中\(\langle . \rangle\)表示对位置\(\mathbf{x}\)的平均。
至此,根据定义,理论上如何用速度场\(\mathbf{u}(\mathbf{x})\)求能谱\(E_k(k)\)已经非常清楚了。但是问题是,根据这个定义进行数值计算的话,2D情况下单单是计算\(R_{ij}(\mathbf{r})\)的时间复杂度就已经是\(O(n^4)\)了!这是因为\(R_{ij}(\mathbf{r})\)本来就是一个二维的场量,而计算其中每个分量又需要对整个\(\mathbf{x}\)做平均。如果是1024*1024的格点,这个时间复杂度是无论如何也算不出来了。。。
正确的算法是这样的:…
曲率辨析
今天才意识到,学物理的人说二维曲面的曲率(curvature)的时候,其实有两种不同的定义… 一种是微分几何里那种定义(Gaussian Curvature);另一种只是简单的定义为曲面函数的拉普拉斯算符(Laplacian)… 而且貌似很多人在说起曲率的时候理所当然的都觉得大家都用的自己的那种定义,而不知道有另外一种定义存在,于是造成了我对这个概念一直以来就有点混乱,现在终于清楚了… 这篇文章稍微详细的辨析一下这两种曲率的定义。
首先我们假定研究的是二维曲面 f(x,y),然后假定曲面上的两个 Principal Curvature 为 \(\kappa_1\)、\(\kappa_2\)。
(1)曲率的第一种定义 Gaussian Curvature 为 \(K_G=\kappa_1*\kappa_2\)。这种定义是微分几何中会见到的定义,这种曲率是 intrinsic 的,是那个跟三角形内角和的大小直接联系的曲面曲率,见 Gauss-Bonnet Theorem。
(2)曲率的第二种定义 Extrinsic Curvature 为 \(K_E=\kappa_1+\kappa_2\)。还有一种与之相关的名称是 Mean Curvature,\(K_M=\frac12(\kappa_1+\kappa_2)=\frac12 K_E\),这二者只相差一个无关紧要的系数。Extrinsic Curvature 有这样一个性质:在曲面的梯度很小这一近似下,Extrinsic Curvature 与 曲面函数的 Laplacian 是相等的,这类似于一维曲线的曲率与二阶导数相等,具体讲解可见…
如何学会打水漂?
//本文是我在知乎上的回答《如何学会打水漂》,后来很荣幸被推荐到了知乎日报《在强大的科学研究指导下,学会打水漂》。
一篇2004年的 Nature 文章[1]里介绍了打水漂的秘诀:神秘角度20°。这篇文章通过系统的实验发现,无论自旋角速度、抛射速度如何,石头与水面的攻角在20°时,石头与水面的接触时间都最少,而该接触时间决定了能量损耗的大小,接触时间越短能量损耗越少,因此20°角是打水漂的关键。注意这里攻角的定义是石头圆盘那个面与水面的夹角,不是入射速度方向与水面的夹角(此角度在15°~40°之间都对结果影响很小)。
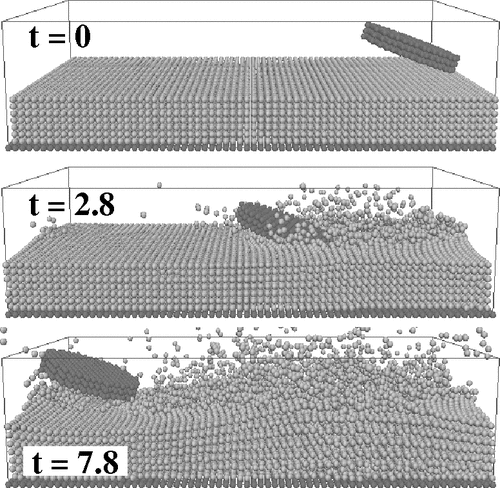
后来一篇2005年的 PRL 文章[2]通过数值模拟重复出了同样的结论,并且给了理论解释。上图出自[2]。…
湍流 Spectrum 与 Cascade 的理解
//本文是我在知乎上的回答《学物理过程中,你有哪些问题是当时理解的比较肤浅,后来突然豁然开朗了?》。
近期在研究湍流有关的东西,就说说对湍流 spectrum 和 cascade 的理解吧。
最初接触湍流的 spectrum 和 cascade 是著名的 K41 Theory (Kolmogorov 1941 Theory) 。针对三维流体,通过假设湍流在小尺度上各向同性,再假设存在一个不是k的函数的常数 energy dissipation rate \(\varepsilon\)(意为单位时间内耗散掉的能量),那么我们可以一定的空间尺度范围内得到三维流体的 energy spectrum:
\[E_k=C\varepsilon^{2/3}k^{-5/3}\]其中k是波数;\(E_k\) 是 energy spectrum,它是能量的傅里叶变换,它与能量的量纲关系为 \([E]=[E_k]*[k]\)(需要注意的是,流体里说的所谓能量其实是通常含义下的能量密度除以质量密度,即 \(E\sim\mathbf{v}^2\),v为速度);C是一个 universal 的无量纲常数。Energy spectrum 的图像如下图(双对数坐标):
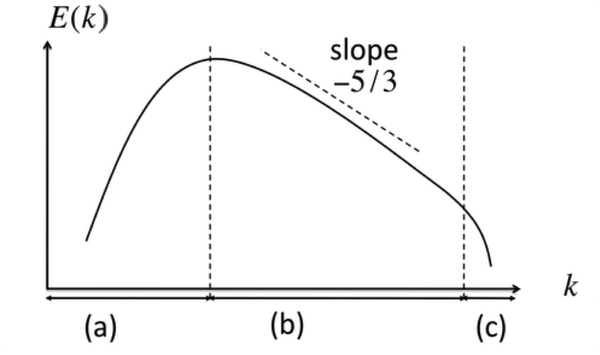
斜率 -5/3 是 K41 理论的著名结论,已经被无数数值模拟所验证。得到这个 …
伯努利方程的适用范围
伯努利方程的适用范围这一问题由上一篇日志《开窗行驶的汽车 车内vs车外哪里压强更高?》所引起。如果按照伯努利方程的话,定常流动的条件要求以车为参考系来分析,所以是车内空气流速小故压强大。这一分析不仅仅是我一个人的答案,在网上搜此问题得到的答案基本都是一样的思路。但是网友@Chengu Wang指出,一篇论文《轿车开窗行驶时的气动阻力分析》里的数值模拟显示,车内空气流速虽然小,但是同时压强也低于车外。这让我深深困惑,因此这几天我自学了一下用Fluent做流体力学的模拟。自己完整地设置了所有条件,确保自己知道自己在干什么,最后得到的结果与前述论文中的相同:车内空气流速小同时压强也小。下图为 流场图和压强图:…


