用凯利判据玩转前文中的“一个有趣的小数学游戏”
在《为什么频繁交易的人大多数在股市上都赔钱了?一个有趣的小数学游戏也许可以解答 》中我写道了如下有趣的小数学游戏:
假设有这么一家赌场提供了这么一个你可以玩无穷多次的游戏:扔一个硬币,若正面向上,则你的资产变成当下的 1.2 倍;若反面向上,则你的资产变成当下的 0.83 倍。你会选择玩这个游戏吗?
在那篇文章中,我做了个简单的模拟,验证了一下这个游戏会出现的结果:绝大多数玩家玩到最后都归零了,只有极少数玩家能够赢得超过本金的钱,而赢得最多的那个人的最终资产远远超过其他人很多很多。
但若改动一个游戏条件,这个游戏就变得更加有趣了:若玩家可以自己选择投注金额呢?玩家应该如何投注才是最佳方案?
直观的想:如果每次都押注100%金额,那其实就回到了一开始那个不能自己选投注金额的游戏,虽然每次玩收益很大,却有非常大的风险最后归零;如果每次都押注太小,那显然回报会很低。最佳的投注比例一定是平衡了这二者的。事实上这个新的游戏的最佳玩法,正是大名鼎鼎的凯利判据 (Kelly Criterion)(阅微堂对凯利判据的讲解也很不错)。凯利判据就是通过最大化资金的log函数的期望而得到的投注比例。证明过程就略过了,基本上就是对这个函数求导就可以。最后得到的凯利判据 (Kelly Criterion)公式为:
K = (pW-qL)/WL
其中p为赢的概率 (0.5),q=1-p为输的概率 (0.5),W为赢的情况下的收益 (0.2),L为输的情况下的损失 (0.17)。在我们这个游戏中,计算得知最佳投注比例 K 约为 0.44。
于是我改动了一下模拟代码,来看看现在用凯利判据投注的话结果如何!
import numpy as np import matplotlib.pyplot as plt |
为什么频繁交易的人大多数在股市上都赔钱了?一个有趣的小数学游戏也许可以解答
今天偶然读到了这篇文章,里面提到的一个简单的小数学游戏相当有意思。
假设有这么一家赌场提供了这么一个你可以玩无穷多次的游戏:扔一个硬币,若正面向上,则你的资产变成当下的 1.2 倍;若反面向上,则你的资产变成当下的 0.83 倍。你会选择玩这个游戏吗?
有两种分析这个游戏的方式。
第一种:不论我玩的时候的本金m是多少,玩下一次的时候,收益的期望总是 m*(1.2-1)*1/2+m*(0.83-1)*1/2。因为赢钱的时候赢 0.2 总是大于赔钱的时候赔 -0.17,所以期望总是正的,那就应该玩,而且要一直玩无限多次。
第二种:若一直玩下去,就会有赢有输,所以应该把 1.2 和 0.83 乘起来看是否大于1。结果是 1.2*0.83=0.996,小于1,因此久赌必输,不能玩。
这两种分析哪一种更有道理呢?大家可以先想想看。
我多年不学数学了,概率论早就忘光了,因此就写了个小代码来模拟一下如果玩这个游戏,会是什么结果。
import numpy as np import matplotlib.pyplot as plt P = 100 # Number of players N |
再贴一道有趣的数学题

上次贴的《一道有趣的数学题》后来在很多人的转帖下火爆了各大平台,看起来很多人都很喜欢这种貌似人畜无害实际凶险至极的小破图😂 这次再来一道,供大家玩味。和上次规矩一样,数学方法或者写程序暴力算都行~
—
更新: https://pub.ist.ac.at/~tbrownin/ 卧槽 上个月还是open question 这就有解了……
网络上的抽奖如何保证公平性
//这篇文章是美国信用卡指南近期搞的一个抽奖活动所使用的方案,原文在这里。
抽奖的公平性向来是抽奖活动中最受人质疑的部分。由于涉及随机数的选取,网上的抽奖活动几乎无法保证公平性,因为很难保证中奖号码是随机生成而非平台人工选取的,也很难保证平台是否删掉了一部分用户的中奖资格而未告知用户。例如:前阵子支付宝锦鲤活动就有人怀疑中奖者是否是钦定的;前阵子王思聪在微博平台上的抽奖,中奖者男女比例为 1:112,甚为蹊跷。
为了解决抽奖公平性的问题,消除暗箱操作的可能性,我们特别设计了以下抽奖过程。
什么样的抽奖是公平的
抽奖过程可以描述为从 0~N-1 (N为奖券总数) 的整数中抽取一个或多个随机整数的过程。除了抽奖算法和抽奖过程需要公开透明之外,一个公平的抽奖过程所使用的随机数(其实是伪随机数)应具有如下的性质:
- 随机数的生成过程不需要依赖于用户对本网站或者任何第三方平台的信任。
- 事先无法预测。
- 事后公开可查。
- 概率上满足均匀分布。
为了保证性质1~3,我们选择使用比特币区块的哈希值来作为我们的随机数种子;性质4只要选取常用的哈希函数即可保证。
我们的抽奖算法
假设奖券编号是连续发放的整数。我们的的抽奖算法如下:
- 选取指定时刻(即抽奖时间)后被挖出的第一个比特币区块的哈希值作为随机数种子,记作 S。
- 用 SHA-256 算法计算 S 的的哈希值 H,然后把 H 作为16进制数字转换为长整数 L。
- W = L % N 为中奖的奖券编号,其中 N
一道有趣的数学题
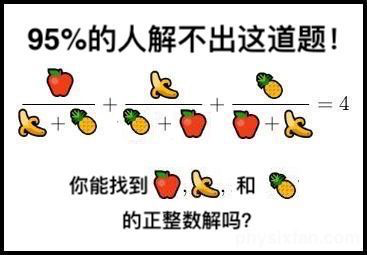
昨天刚看见的数学趣题,是我近期见过的最有意思的了!大家可以尽管尝试一下,数学方法或者写程序暴力算都行~ 保证解是存在的。
解法见这个链接,不过最好先自己想想,实在不行了再点开看,否则会丧失乐趣:https://www.quora.com/How-do-you-find-the-positive-integer-solutions-to-frac-x-y+z-+-frac-y-z+x-+-frac-z-x+y-4…
五子棋/连珠近况简介
五子棋作为一个规则简单易懂、入门门槛低的棋类,我想同年龄段的很多人都曾下过吧。不过相信大多数人跟我一样,都没有对五子棋有过专业的研究,当时只是下着玩而已。估计很多人都听说过五子棋黑棋必胜所以五子棋被终结了的传言,也有很多人认为计算机AI可以在五子棋上很轻易的下过人类吧,不过这几天我看了看五子棋/连珠的一些最新近况,过去确实曾对五子棋产生过一些误解,而且最近几年五子棋AI也有了较大的进步。我虽然不是专业人士,但是最近看到了一些网上靠谱资料,在这里给大家简介一下吧,如果有错误请告知!
首先要做一些名词解释。五子棋(Gomoku)现在特指无禁手类的规则,而有禁手类的规则现在被称为连珠(Renju),下文中将区分对待这两个词。禁手(Disallowed moves)的意思是,如果黑棋(原始规则下的先手)下出了双活三、双四或者长连,那么算黑棋输。显然,禁手是对先手优势的一种平衡措施。
黑棋必胜是真的吗?原始规则下,无论有没有禁手,答案都是,是的。对于五子棋(Gomuku,无禁手),1992年Victor Allis已经证明黑必胜的,文章在这里;对于连珠(Renju,有禁手),2001是Janos Wagner第一次证明的黑必胜的,文章在这里。当然,早在这两篇论文很久很久之前,五子棋界就已经通过经验知晓这一事实了,只是最近才有人真的用计算机穷尽了所有可能性证明这一命题为真了而已。我想应该下过五子棋的很多人都听说过所谓的“花月”“蒲月”必胜开局吧,说的其实就是这回事。
那么我们知道黑棋必胜之后,五子棋/连珠就被终结了吗?从某种意义上来说,原始规则下的五子棋/连珠确实是被终结了,但是,通过修改规则,五子棋/连珠仍然可以作为一个正规的职业比赛继续生存下去,下面就分别简介一下国际上正式比赛用的规则:
一、五子棋规则:
- 黑白双方轮流落子。
- 首先在横、竖、斜方向上成五(连续五个己方棋子)者为胜。
- 超过五子以上不算赢也不算输。
在五子棋规则基础上,还有一些细分的规则,目前(2014年)国际上比赛采用的规则为 Gomoku swap 2 规则。
Gomoku swap 2:
- 假先在棋盘任意下三手(二黑一白)假后方有三种选择:(1)选黑;(2)选白;(3)下四、五两手(一黑一白)再假先方选择黑或白。
- 此后按 Gomoku 规则继续进行。


