号称可能挑战Google霸主地位的WolframAlpha今天问世
http://www.wolframalpha.com 今天问世了。
这是一个传说中的下一代搜索引擎,还号称有可能挑战Google的霸主地位。WolframAlpha的搜索和现有的搜索引擎完全不同,现在的搜索引擎会返回许许多多包含关键字的网页,但是WolframAlpha会直接返回问题的答案。以前在Scientific American上面看到过文章说以后的搜索引擎的发展方向就是这样,今天算是第一次亲眼见到了。
Wolfram是一个很强的人也是一个很强的公司,反正我以前一直比较膜拜的Mathematica就是Wolfram公司出的。据称WolframAlpha背后有一个强大的数据库以及Mathematica的强大计算功能保障返回问题的答案。
今天我去体验了一下下。
搜索我的出生日期“Sep 2 1990”:结果有很多,其中有一条是6831 days ago,显示出我活了多少天了。可惜Notable events for September 2, 1990里面什么也没有,希望过几年之后里面能写到A famous Chinese FX was born…哈哈
搜索我的城市”Qingdao”:结果显示出青岛有1.642 million people,海拔40m,显示出现在的气温是15摄氏度(去浙大上预科的同学要气疯了),湿度82%,风速2 m/s…
搜索我最崇拜的人”Feynman”:full name | Richard Phillips Feynman;date of birth | 1918-05-11 (91 years ago);place of birth …
关于e、Pi和整数之间关系的重大发现
今天我偶然的发现了这样一个令人吃惊的事实:数学中最重要的两个无理数e和Pi居然和整数有一个绝妙的联系,请看下式:
$$e^{\sqrt{163}\pi}=262537412640768744$$
等式的右边居然是一个整数!
当然这个等式用中学统一发的小计算器是验证不了的,因为显示位数不够;Windows自带的那个傻乎乎的计算器貌似也不行,除非你给出足够精确的Pi的值。如果你安装了Mathematica的话可以进行简单的验证,比如N[E^(Sqrt[163]*Pi), 20]或者N[E^(Sqrt[163]*Pi), 25]等等,可以验证这样一个惊人的等式。…
趣题:求两圆柱相交部分的体积
昨天去图书馆看趣味数学大师马丁加德纳的小册子《意料之外的绞刑》,看到了这个趣题:求两圆柱相交部分的体积(两圆柱半径都为1)(正交)。要求是不用微积分,只用高中生就能看懂的简单数学。如果你难以想象那部分到底是个什么形状,下面这幅图可以帮帮你。
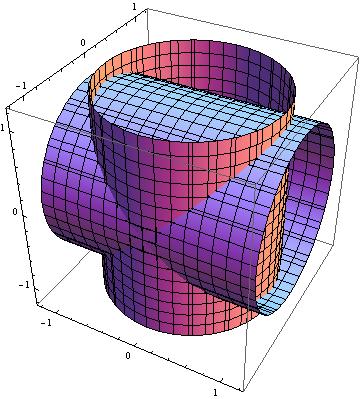 …
…
迭代法求平方根
很久以前看过求平方根的这么一个方法,是用的迭代,按下面这个公式进行迭代即可求出a的平方根:
Xn=(Xn-1+a/Xn-1)/2 (n>0)
其中X0可以随便取一个数。当Xn-Xn-1满足精度要求时,即可输出Xn作为答案。
很长时间以来都想不明白,为什么通过这样的迭代会算出平方根。上网查他的原理也没查到。最近在《边缘奇迹——相变与临界》上看到了重正化群中类似的东西,我恍然大悟,想到了怎样来理解。
我们画出y=(x+a/x)/2的图像,再在同一坐标系内画出y=x。如下图(a=2):…
一个有趣的级数
估计有不少人知道这样一个公式,1-1/3+1/5-1/7+1/9-…=π/4
我很小的时候就见过这个,貌似叫莱布尼茨公式,觉得相当有意思,一些自然数的加减乘除居然出现了π!之后我对这个公式思考了好长时间,总是想不出来怎么来证明。我一直把这个问题记在心里,期盼着那一天能找到他的证法。
我曾经专门找过微积分的书和有关级数的数,遗憾的是,这么经典的一个无穷级数求和居然都没有写到。我近日在数学吧问了一下,好象没有初等数学的证明,有人贴出来了一个不过我没看明白。
有意思的是,今天在读《费曼物理学讲义》有关谐波的章节时,居然看到了这个等式的证法!呵呵,我都惊喜得不行了,居然在经典物理书里面看到了有意思的数学证明!我想把这个证法贴出来,供大家欣赏,相当精彩啊,不过没学过微积分的就不用看了。…

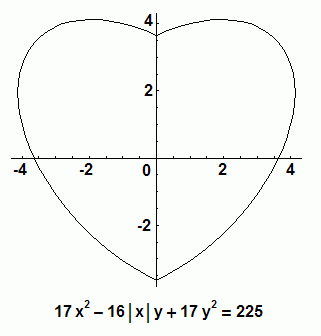 …
…
