初等数学证明开普勒第二定律
开普勒第二定律是这么说的:在相等的时间内,行星与恒星的连线扫过的面积相等。当我第一眼看到这条定律的时候,觉得非常神奇,而当我看到了这个定律的证明时,不禁更觉神奇了!下面我把从《物理定律的本性》上看到的关于这个定理的证明简要写下来供大家欣赏。
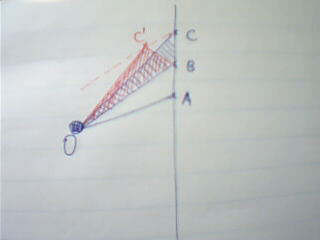
如图,O为恒星,直线AC为行星不受引力时的轨迹。设行星从A到B、从B到C所用的时间间隔Δt相等,A处的时刻为t1,B为t2,C为t3。现在假设行星不受O的引力作用,那么这时扫过的面积SΔABO和SΔBCO相等(等底同高)。现在行星受到引力作用了,因为引力的方向时刻指向恒星,所以在从t1到t3这段时间里,行星所受的引力的方向的总效果应该沿着BO方向(这需要一点向量的知识)。因此,t3时刻行星的位置C’应该由两个向量相加而得到:向量AC+向量CC’(作CC’平行于BO,因此沿BO方向的向量等价于CC’)。这样,SΔBCO=SΔBC’O(同底等高)。因此,SΔBC’O=SΔABO。因为Δt是任取的,所以在相等的时间内,行星与恒星的连线扫过的面积相等。
 …
…


