初等数学证明开普勒第二定律
作者： physixfan
开普勒第二定律是这么说的：在相等的时间内，行星与恒星的连线扫过的面积相等。当我第一眼看到这条定律的时候，觉得非常神奇，而当我看到了这个定律的证明时，不禁更觉神奇了！下面我把从《物理定律的本性》上看到的关于这个定理的证明简要写下来供大家欣赏。
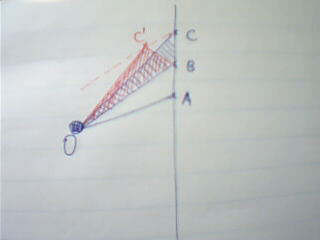
如图，O为恒星，直线AC为行星不受引力时的轨迹。设行星从A到B、从B到C所用的时间间隔Δt相等，A处的时刻为t1，B为t2，C为t3。现在假设行星不受O的引力作用，那么这时扫过的面积SΔABO和SΔBCO相等（等底同高）。现在行星受到引力作用了，因为引力的方向时刻指向恒星，所以在从t1到t3这段时间里，行星所受的引力的方向的总效果应该沿着BO方向（这需要一点向量的知识）。因此，t3时刻行星的位置C’应该由两个向量相加而得到：向量AC+向量CC’（作CC’平行于BO，因此沿BO方向的向量等价于CC’）。这样，SΔBCO=SΔBC’O(同底等高)。因此，SΔBC’O=SΔABO。因为Δt是任取的，所以在相等的时间内，行星与恒星的连线扫过的面积相等。
6 Comments
Post a comment
牛顿的《自然哲学的数学原理》也有
easy’…
这个证明有问题，受引力影响下t2时刻行星并不位于B点啊，也不在BO上，因此SΔBC’O=SΔABO无意义
所以在从t1到t3这段时间里，行星所受的引力的方向的总效果应该沿着BO方向（这需要一点向量的知识）这段能在解释一下吗？我没想明白，这里的行星在这上面是连续运动的，我没想明白，是直接求平均吗？
如果把行星轨道近似圆