倒立单摆的稳定性与Ponderomotive Force
众所周知,单摆有两个平衡点,一个是垂直向下的稳定平衡点,另一个是垂直向上的不稳定平衡点。然而,只要在单摆的悬挂点处施加一定条件的振动,无需任何反馈系统,就可以让向上的平衡点也变成稳定的!下面这个视频就演示了这一个神奇的现象。(原视频地址为http://www.youtube.com/watch?v=5oGYCxkgnHQ 在墙外…)
这个现象要如何解释呢?一定要注意,这个悬挂点的振动没有依赖任何反馈装置,跟很多工科院系做的横向移动的小车上的倒摆有着本质的不同。显然不是随便一个振动都能稳定住倒立单摆,那么这个振动到底需要满足怎样的条件才可以呢?这个问题的关键,叫做Ponderomotive Force,中文翻译是“有质动力”。中文世界里对Ponderomotive Force的涉及是如此至少,以至于我这个学了四年本科物理的人都完全没有听说过它的中文版本,因此我决定写此文科普一下。
首先给出一个直观而不定量的理解。倒立单摆的情形可以直观地看作一个小球在一个碗里运动,碗的形状即势能:
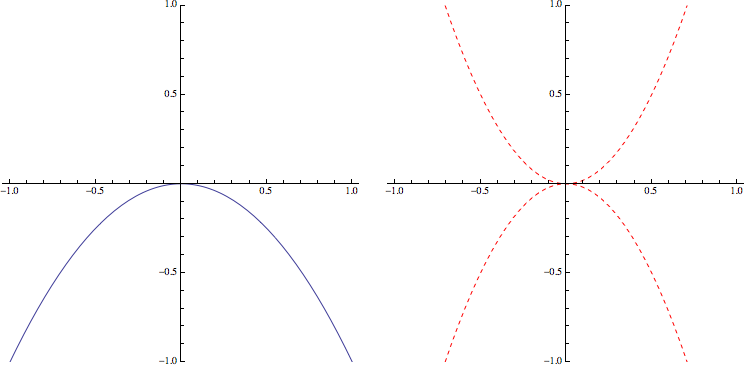
在没有振动时,倒立单摆所处位置的势能形状如左图所示,在其中运动的小球随便一偏移,就会越滚越低。而加上振动之后,如果把悬挂点作为参考系,那么倒立单摆此时会受到一个惯性力产生的正负震荡的新势能,其形状如右图所示。如果震荡的幅度合理,而且频率足够高,那么两个势能叠加起来的结果就可以是:小球在一个振荡周期内的一部分时间的确有下滚的趋势,但是还没来得及滚多远,碗的形状就变了,又把它给托起来让他回去了。最终的效果就是,倒立单摆被稳定住了。
下面开始详细的定量计算:
/******************大量方程插入的分割线******************/
我们先直接来研究一个一般的情况,然后代入倒立单摆的具体情境。此类问题一般的方程为
\[m\ddot{x} = -dU/dx+f \]
当没有最后一项\(f\)时,就是个普通的小震动的方程,设其固有频率为\(\Omega\);\(f\)是一个高频的震荡项,其表达式可以一般地设为
\[f=F_1(x)\cos\omega t+F_2(x)\sin\omega t\]
其中\(\omega \gg \Omega\)。
解这个方程的关键,在于分离快、慢两个不同时间尺度的运动。为此,设\(x\)为
\[ x=x_0(t)+\tilde{x}(t)\]
其中\(x_0(t)\)为慢时间尺度项,而\(\tilde{x}(t)\)为快时间尺度项,设此快时间尺度项相对于慢时间尺度项为小量。代入原方程,并且近似到\(\tilde{x}(t)\)的一阶:
\[m(\ddot{x}_0+\ddot{\tilde{x}} )=-dU/dx_0-\tilde{x} d^2U/dx_0^2+f(x_0)+\tilde{x}\partial f/\partial x_0\]
这个方程里既包含慢项也包含快项。所有不含\(\tilde{x}(t)\)和\(f\)的项均为慢项,而所有含有\(\tilde{x}(t)\)和\(f\)的一次项的都是快项。那最右那一项,包含了二者的乘积,是快还是慢的呢?答案是:慢的!原因可以理解为\(\sin^2\omega t\)的平均值(在一个周期内的积分)并不是零。这一项对慢时间尺度的运动产生了贡献,正是Ponderomotive Force的关键所在!
对上式做平均,消掉所有快时间尺度项,可以得到慢项的运动方程:
\[m\ddot{x}_0=-dU/dx_0+<\tilde{x}\partial f/\partial x_0>\]
想要继续求解上式,需要把最右一项的具体形式解出来,即需要找到\(\tilde{x}(t)\)和\(f\)的联系。用包含了所有项的方程减掉慢项的方程,即可得到快项的方程:
\[m\ddot{\tilde{x}}=-\tilde{x}d^2U/dx_0^2+f(x_0)\]
由于\(\omega \gg \Omega\),等式右边第一项远小于等式左边一项,因此略去。因此容易解得
\[\tilde{x}=-f(x_0)/m\omega^2\]
有了这个关系式,就容易计算\(<\tilde{x}\partial f/\partial x_0>\)了。最终,慢时间尺度的运动方程为:
\[m\ddot{x}_0=-\frac{d}{dx_0}(U+\frac{1}{4m\omega^2}[F_1^2(x_0)+F_2^2(x_0)])\]
最右那一大坨和\(U\)加在一起的,就是Ponderomotive Potential,而它的梯度,就是Ponderomotive Force:
\[F_{pond}=-\frac{1}{4m\omega^2}\frac{d}{dx_0}[F_1^2(x_0)+F_2^2(x_0)]\]
其物理含义,就是一个高频震荡的力最终可以产生一个慢时间尺度上的力,这个力就称之为Ponderomotive Force。
再回到倒立单摆的具体问题上来。当总势能的二阶导数在倒立的位置上大于0时,那么倒立单摆将稳定。只有重力势能的时候是不可能的,而Ponderomotive Potential的加入则使之成为可能。现在研究一下在什么条件下可以稳定。设悬挂点在垂直方向是振动频率为\(\omega\)振幅为\(Y\)的简谐振动,单摆的摆动角度为\(\phi\),可以直接带入上面的一般情况的结果而得到
\[U_{pond}=\frac14m\omega^2\frac{Y^2}{l^2}\sin^2\phi\]
通过在\(\phi=\pi\)处势能之和二阶导数大于0可以容易的得到倒立单摆稳定条件:
\[\omega^2Y^2>2gl\]
除此之外当然还得有\(\omega \gg \Omega=\sqrt{g/l}\),这两个条件都满足的情况下倒立单摆就可以稳定了!
/******************方程结束的分割线******************/
Ponderomotive Force还有许多其他有意思的应用。去年我在普林斯顿等离子体实验室里就看到了一个相关的演示实验:他们的实验装置可以让一些带静电的面粉稳定的悬浮在空中。如果只是静电场的话,可以证明在一个空腔内部无论如何布置电场都不能形成一个下凹的势。因此为了形成稳定平衡,必须借助Ponderomotive Force,用高频振荡的电场最终产生一个慢时间尺度上的新势能来使之成为稳定平衡。那个组其实在研究如何利用Ponderomotive Force来稳定地约束受控核聚变装置里的高温等离子体,也许将来可以发挥很大的作用呢~



U_{pond}那个方程,是不是不应该有分母上的l^2?否则量纲不对呀。
受教了 不明觉厉
我本科毕业设计就是倒立摆的模糊神经网络算法。。。。。查了很多资料但都没听说有质动力这个东东。回家以后好好看看。从这空间学到了很多东西。话说毕设做那个不是小车的,是旋臂式的。
哈哈,我今天也刚在博客写了一篇倒立摆的博文~http://www.kylen314.com/archives/4139
去前辈博客学习学习哈
好神奇啊。。。
好神奇
我想可以这样直观定性理解:把惯性力简化为前半段的F(向上)和后半段的-F,假设初始速度为零或指向平衡点。合力是前半段F-G和后半段-F-G,前半段要小2G;然而计算合力矩时对应的矢径也在变化,前半段的矢径总要比后半段大一些,这个差别我们用前半段的矢径变化量来估计,这个变化量是O(F)的量级。所以只要F>>G,总的结果就是单摆位置朝平衡点又近了一步,而且还多出一个朝向平衡点的角动量。假设初速度背向平衡点,如果前半段结束时F能把单摆拉回原位,整个过程就适用于上面的分析。这说明初速度的干扰不能超过某一阈值(与F/ω有关)。(存在这样的情况:F没能把单摆拉回原位,但整个过程恰好形成一个循环。大尺度来看单摆稳定在这个角度上。当然这是个不稳定平衡,对应着有质动力与重力合力恰好沿摆棍方向的情况。)最后感谢博主!今天又学到了新姿势!
我是来看视频的公式太复杂不看了
我感觉,楼主分析得不是十分准确,通过结合计算机,我得到了更宽松的下限,请楼主请一下http://spaces.ac.cn/index.php/archives/2277/
我们很实现往一个系统加入一项纯粹的力吧?我觉得应该是加入一项振荡的势或者是将装置放到一个非惯性系中从而得到一项额外的力。这样子的话,多增加的一项应该类似f(t)*x这样的形式的,而不是单纯的f(t)
赞!!