北京大学2008年保送生和自主招生数学试题答案
北京大学2008年保送生和自主招生数学试题解答
这套题的难度还是相当大的,这里的解答也不是我一个人做出来的,有我自己做的,有同学帮着做的,也有网上的解答。在网上我还没发现这套题目的完整解答,所以我写了这篇Blog,希望对众多有意考北大的人能够提供一些帮助。
1.证明:边长为1的正五边形的对角线长为(1+√5)/2
证明:经鉴定,这是一道初中数学题,我就不写详细的解答了,用相似三角形就证出来了。
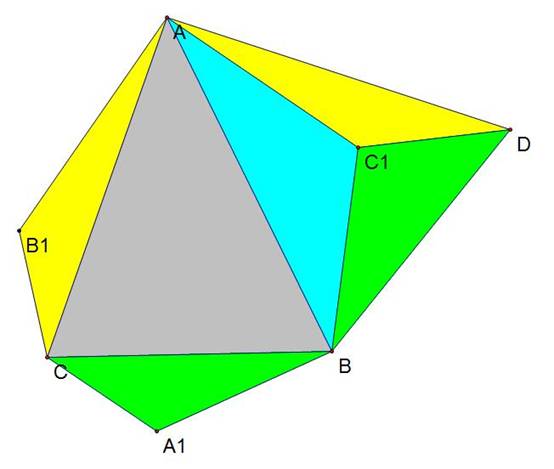
2. 已知一个六边形AB1CA1BC1,AB1=AC1,CB1=CA1,BA1=BC1,∠A+∠B+∠C=∠A1+∠B1+∠C1。证明:三角形ABC面积为六边形的一半。
证明:如图,把三角形AB1C转至AC1D的位置,连接BD,则很明显三角形BDC1与三角形BA1C全等,所以三角形ABC和三角形ADB全等,故三角形ABC面积为六边形的一半。
且min{a1, a2, a3}≤min{b1, b2, b3}
证明:max{a1, a2, a3}≤max{b1, b2, b3}。
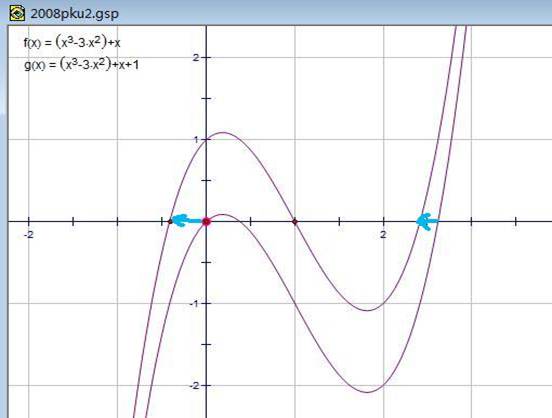
证明:令a1 a2 a3为y=x^3+px^2+qx^1+m的三根
则b1 b2 b3可以是y=x^3+px^2+qx^1+n的三根(三次方程的韦达定理)
两曲线仅仅是上下平移的关系
显然当最小根左移时最大根也左移
解:设北方球队共有x支,则南方球队有x+9支
所有球队总得分为![]()
南方球队总得分为![]()
北方球队总得分为![]()
南方球队内部比赛总得分![]()
北方球队内部比赛总得分![]()
![]()
解得:![]()
因为![]() 为整数
为整数
x=6或x=8
当x=6时
所有球队总得分为![]() =210
=210
南方球队总得分为![]() =189
=189
北方球队总得分为![]() =21
=21
南方球队内部比赛总得分![]() =105
=105
北方球队内部比赛总得分![]() =15
=15
北方胜南方得分=21-15=6
北方球队最高得分=5+6=11
因为11×15=165<189
所以南方球队中至少有一支得分超过11分.
冠军在南方球队中
当x=8时
所有球队总得分为![]() =300
=300
南方球队总得分为![]() =270
=270
北方球队总得分为![]() =30
=30
南方球队内部比赛总得分![]() =136
=136
北方球队内部比赛总得分![]() =28
=28
北方胜南方得分=30-28=2
北方球队最高得分=7+2=9
因为9×17=153<270
所以南方球队中至少有一支得分超过9分.
冠军在南方球队中
综上所述,冠军是一支南方球队
这道题目前我还不会做,我认识的人也都不会做,在网上也没有找到答案,希望会做的网友能够提供牛解…



最后一道是不是该注意这么几个字:不透光的几何体。
我注意到了,可是依然完全不会做…
那个点光源发射到 xy 平面上的光,永远不会在 y > 0 的区域出现,永远可以在 y <= 0 的区域出现。
因此,那个被照亮的部分长度为 2π 的圆弧,其实就是半个圆,是故未被照亮的部分的长度也是 2π。
哦,抱歉,粗心了,没这么简单,我再想想。
我想这样应该可以:
(1)由于光源点 P 在抛物体底面的边缘上,它在 xy 平面上的照射范围由该点的切平面和 xy 平面相交的直线限定,所以关键是求切平面与 xy 平面的交线。 当然,只利用高中知识。 显然切平面上过 P 点的任一直线都是抛物面的切线,所以我们只需求出两条不同方向的切线,它们分别与 x 轴, y 轴相交。 这个交点容易求,一个是通过求圆的切线,一个是通过求抛物线的切线(如果不懂微分,至少知道抛物线聚焦的性质,可以用它求切线)。
(2)题目其实是让我们求照射圆的半径,稍作思考,可知这个圆和上面求出的分割线要在 xy 平面上的第一象限有两个交点,接着容易得出关于半径 r 的方程。如果我没算错的话,方程应该是 rSin(π/r) = 4/sqrt(5),数值解约为 1.81268,未被照亮的长度约为 5.10624。
(3)如果错了,请不要鄙视我……
原来我第一次看这个题的时候看错题了…
你说的挺有道理的,我在研究研究
“rSin(π/r) = 4/sqrt(5)”
可以得到这个是对的,但估计不是这样做,我也想想。。
ps:我比楼主大一届,兴趣在数学上,有机会交流交流
利用偏微分应该可以得出上面的结果,但是我解不出来……当年做自招题的时候就卡在这里了……应该有巧解,仁兄到了北大问一问。偏微分做这道题还算好用,没什么思维技巧。
另:佩服仁兄,小弟是清华的保送,本想报数学或物理,但是家里非要让我学工科,所以很羡慕仁兄……当然,你的分数我就是去考北大也比不上……佩服
不知道那个数值解能不能用式子表示?
我也只做出了前4道题
5.应该2派吧
要讨论吧1.r(4/sqrt5)矛盾 不可能·· 2.r>(4/sqrt5)时 就超麻烦了 要用反三角函数了吧…… 就是平面上一个三边为2、4、2sqrt5 的三角形 直角顶点为圆心 交来交去的 结果没算出来 哎……
第三题我也是用图像解的,但我觉得用图像做证明题不是很漂亮,不严密吧,有没有更好的解法
关于第3题有严格证明法,可以证明f(x)=0在(b3,+infty)上无根……
第四题,小弟最后弄出来个解不出来的的超越方程……
关于最后一题,我这么想的:只要得到电光源可照亮的区域(在xy平面内),就可以把问题化简为2维平面的几何题了。(点光源能照亮的区域也很好判断,就不提了,而那个圆的半径也肯定是大于根号二的)我的思路是这样的,求出点光源处的几何体的法线矢量,那么过光源且垂直于此法线的平面必然与xy平面有条交线。这条交线很容得到:与发现垂直且过点光源的平面上的点与点光源形成的矢量垂直于法线,所以一下就得到此平面,然后只需令z=0即可。至此,问题已经从3维化简为2维的了。剩下的就简单了。
我说一下我对最后一道题的计算。光源正好在遮挡物体上,那光线被物体遮挡,相当于被过那个点的切面遮挡,有两个切面,一个显而易见是y=0平面。另一个是抛物面的切面。由于要确定XY平面内能被照亮的地方,所以只要确定这个切面和XY平面的交线即可。应该很容易可以找到(0,2^1.5)和(2,0)两个交点,这样这条交线也就确定了。可以确定y<0的半个圆一定会被照亮,另外,可能在上面的切线外侧有一部分会被照亮。如果只有半圆被照亮,那么r<(8/3)^0.5,这样照亮的地方不足2*pi。另外,显然r<2,所以不足以使得上面两段区域连起来,所以只能是一个半圆区域和一段弧。2*pi=pi*r+2r*arccos((8/3)^0.5/r),大概数值得到r=1.6986,未照亮部分大概4.3894。
你们都是什么神人阿
老子看到了人与人的差距···