细推物理须行乐 何用浮名绊此身
Search
-
Recent Posts
Random Posts
Tags
Links
我首先要证明,面积最大的图形满足一个性质:一条平分周长的直线(暂且把它叫做周长平分线),一定也平分面积。因为,如果不平分面积的话,那么我总可以把面积较大的那块翻到另一边去,使得周长不变,而面积增大(如左图,红色曲线围成的面积大于蓝色曲线)。好了,接下来,我要再证明面积最大的图形满足第二条性质:周长平分线与曲线的两个交点和曲线上任意一点构成的三角形,必然是直角三角形。因为,如果它不是直角三角形,我可以把他拉伸或压缩一下,使它成为直角三角形,这样新三角形的面积大于原三角形的面积(证明省略,主要使用S=absinθ/2),而图形其他部分面积不变,这样面积就扩大了。因此,面积最大的图形满足上述两条性质,我们就不难推出它是圆了。
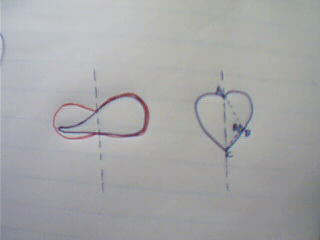
physixfan
eaglefantasy
Eagle_Fantasy
宇宙的心弦
Traction Theme by The Theme Foundry
Copyright © 2025 physixfan. All rights reserved.  宇宙的心弦 by physixfan is licensed under a Creative Commons Attribution-NonCommercial-NoDerivatives 4.0 International License.
宇宙的心弦 by physixfan is licensed under a Creative Commons Attribution-NonCommercial-NoDerivatives 4.0 International License.
Necessary cookies are absolutely essential for the website to function properly. This category only includes cookies that ensures basic functionalities and security features of the website. These cookies do not store any personal information.
Any cookies that may not be particularly necessary for the website to function and is used specifically to collect user personal data via analytics, ads, other embedded contents are termed as non-necessary cookies. It is mandatory to procure user consent prior to running these cookies on your website.

其实我看到过一个证明说,周长相等的前提下,凸多边形比包在它内部的凹多边形大,
可不可以用这个证明然后极限一下呢?
具体完整严谨的过程应该不会太简单吧…
第一个已经证明面积最大他就有无穷个对称轴,就是圆了。第二个证明为直角三角形的证法有问题吧?
第一条性质说的是平分周长的线一定平分面积,这并不等价于有无穷多个对称轴,比如正方形就满足上面说的性质。
第二部分说的不算好,这样看确实有问题。我的意思其实是,只拉伸或压缩三角形,而保持其他部分不变…可能说的还不算明白,不过网上能找到关于这个问题的比较好看的图也许会帮你理解
其实你首先需要证明这个极限的存在性。
微分几何里好像给了一种挺好玩的证明,记不清了
用傅立叶级数+Parseval identity,很快很快……(Stein的《傅立叶分析导论》)
为什么有点不严谨的感觉……
感觉只需要第一个证明就好了,随意在图形上面选一个点总可以找到另外一个点平分这个图形的周长,这两个点连线又是对称轴,然后第一个点选定是随意的,所以存在无穷多对称轴
不详之处:1 在你的调整过程中将出现比圆大的图形2 在你的调整过程中原先的直角变没有,你还需要调整3 圆符合你的不规范条款并不能说明圆最大你的证明和Jakob Steiner基本一样,都有巨大错误。这是我的证明user.qzone.qq.com/2941039326
严谨的证明也很简单。http://user.qzone.qq.com/2941039326
因为大量没有直角三角形的图形比有直角三角形的图形大,把图形调整成直角三角形只是比调整之前大,可是调整之后可以把直角三角形调没但还是更大。没有证据表明有直角三角形的图形比任何图形大,所以不能确认直角三角形是最大的图形。他不敢限制其他角度一起调整,限制了就不是任何图形了。所以以他的方法判断最大图形是不恰当的。
前人(这个前人是说比我老的,不是说比Steiner老)就有这个证明:先证明等周的图形都有个有限的面积,后面的证明就是史丹纳。我想问,图形在被调整得越来越大的过程中(就是把图形里面的非直角三角形调整为直角,交换使图形对称……),他能够简单的说出每一次增大的面积加起来能够达到等周情况下圆的面积吗?打个比方,圆周率小数点后每一位加起来永远也达不到3.2,而只能说位数越多越接近,但永远达不到。你所知道的最简单的等周定理是什么?
原来这里的回复时间可以自行修改的