庞加莱的几何学
最近在看庞加莱(Poincaré)(又被翻译成彭加勒)的《科学与假设》,这是一本闪耀着思想光辉的圣书。介绍科学知识的书很多很多,但是像《科学与假设》这种写科学哲学的书恐怕很难找得到。虽然这本书的语言非常艰涩难懂,但这本书我至少读过3遍,每一遍都能读出一些新的感悟。
在这本书里,庞加莱对几何学提出了几条思想很深刻的见解:
1.几何学公理既非综合判断,也非实验经验,他们是约定。约定是心智的产物,约定的选择是自由的,但又不是随意的。
2.假使自然界没有固体,便不会有几何学。欧几里德几何学的性质与天然固体非常符合。
3.欧几里德几何学不比非欧几何学更真,他只是更为方便而已。经验在任何时候都不会与欧几里德共设相矛盾,同样任何经验永远也不会和罗巴切夫斯基共设相矛盾。
4.可以建立一本词典,把非欧几何的术语和欧几里德几何的术语之间建立一一对应的关系,这样非欧几何将永远不会和欧几里德几何相矛盾。
5.实验告诉我们的是物体之间的相互关系;至于物体与空间的关系,或者空间个部分的互相关系,没有一个实验影响或者能够影响。实验与空间无关,而与物体有关。
为了对非欧几何加以诠释,庞加莱在这本书里提到了著名的庞加莱圆盘模型,这个模型是非常有意思的:
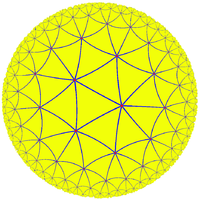 …
…
埃舍尔的数学艺术
20世纪的伟大艺术家埃舍尔(Escher)是个与众不同的画家,是个和我差不多的数学Geek。他的所有艺术品都不是通常的画作,而是充满数学气息或者是现实中不可能的视觉错觉作品。在所有艺术家中,我最欣赏的就是埃舍尔,甚至甚于达芬奇。虽然埃舍尔的作品初期被当作异类来排斥,但是随着岁月流逝,越来越多的人狂热的喜爱起了他的作品,尤其是对数学有癖好的人。这篇文章将带着大家看看埃舍尔是如何将数学与艺术完美结合。
给大家展示的第一幅画叫《天使与魔鬼》,是我见过的最强的艺术品。这不是一个普通的圆,而是一个非欧几何空间,最早是由庞加莱(Poincaré)(又被翻译成彭加勒)提出了这个模型(参看我的这篇文章)。而填充整个非欧几何空间的,居然是有着强烈反差的白色天使和黑色魔鬼,真是绝了!
 …
…
圆的弦比内接正三角形之边大的概率是多少?
 圆的弦比内接正三角形之边大的概率是多少?
圆的弦比内接正三角形之边大的概率是多少?
偶然间从庞加莱(Poincaré)(又被翻译成彭加勒)的《科学与假设》的概率演算这一章看到了这个命题,他最早由贝特朗提出,故又叫做贝特朗悖论。这一问题有三种解答,答案分别是1/2、1/3和1/4,我怎么也想不清楚到底哪一种是对的,其他的为什么错了,请路过的大牛们帮忙看一看。
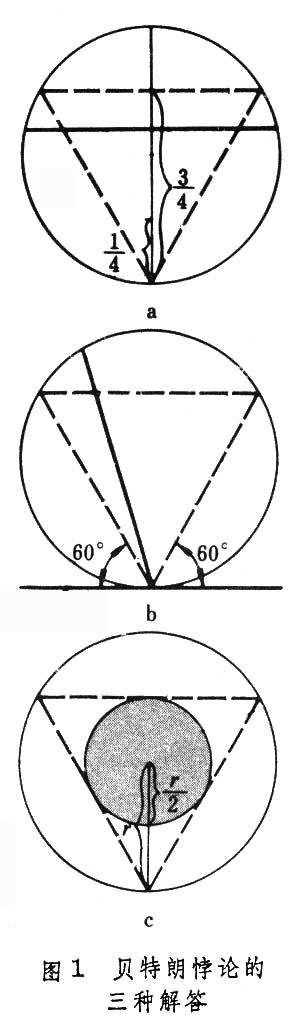
解法一:由于对称性,可预先指定弦的方向。作垂直于此方向的直径,只有交直径于1/4 点与 3/4 点间的弦,其长才大于内接正三角形边长。所有交点是等可能的,则所求概率为1/2 。
解法二:由于对称性,可预先固定弦的一端。仅当弦与过此端点的切线的交角在60°~ 120° 之间,其长才合乎要求。所有方向是等可能的,则所求概率为1/3 。
解法三:弦被其中点位置唯一确定。只有当弦的中点落在半径缩小了一半的同心圆内,其长才合乎要求。中点位置都是等可能的,则所求概率为1/4。
这个问题的答案到底应该是多少呢?
顺便说一下,《科学与假设》里有一个观点我很认同,他觉得古典概型中概率的定义不严谨。定义:“若只有有限个不同的基本事件,且每个基本事件发生的可能性是均等的,则事件A的概率等于事件A包含的基本事件数除以基本事件总数。”可是,定义中出现的“可能性是均等的”如何判断?这是不是用概率来定义概率了?这样的定义不算循环定义么?
注:文中的三种解法及图片来自百度百科。…


