细推物理须行乐 何用浮名绊此身
Search
-
Recent Posts
Random Posts
Tags
Links
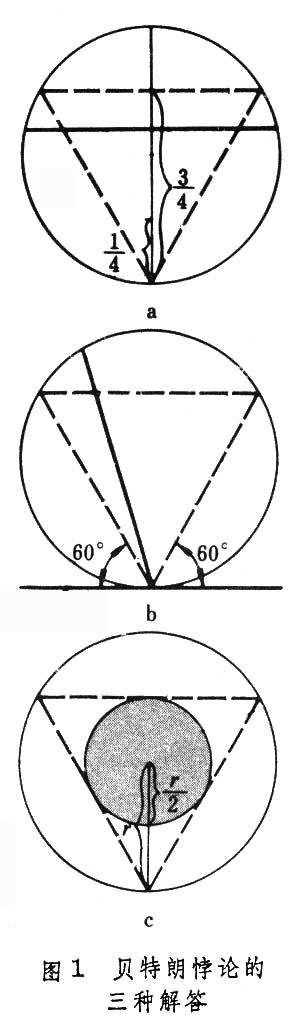 圆的弦比内接正三角形之边大的概率是多少?
圆的弦比内接正三角形之边大的概率是多少?
偶然间从庞加莱(Poincaré)(又被翻译成彭加勒)的《科学与假设》的概率演算这一章看到了这个命题,他最早由贝特朗提出,故又叫做贝特朗悖论。这一问题有三种解答,答案分别是1/2、1/3和1/4,我怎么也想不清楚到底哪一种是对的,其他的为什么错了,请路过的大牛们帮忙看一看。
解法一:由于对称性,可预先指定弦的方向。作垂直于此方向的直径,只有交直径于1/4 点与 3/4 点间的弦,其长才大于内接正三角形边长。所有交点是等可能的,则所求概率为1/2 。
解法二:由于对称性,可预先固定弦的一端。仅当弦与过此端点的切线的交角在60°~ 120° 之间,其长才合乎要求。所有方向是等可能的,则所求概率为1/3 。
解法三:弦被其中点位置唯一确定。只有当弦的中点落在半径缩小了一半的同心圆内,其长才合乎要求。中点位置都是等可能的,则所求概率为1/4。
这个问题的答案到底应该是多少呢?
顺便说一下,《科学与假设》里有一个观点我很认同,他觉得古典概型中概率的定义不严谨。定义:“若只有有限个不同的基本事件,且每个基本事件发生的可能性是均等的,则事件A的概率等于事件A包含的基本事件数除以基本事件总数。”可是,定义中出现的“可能性是均等的”如何判断?这是不是用概率来定义概率了?这样的定义不算循环定义么?
注:文中的三种解法及图片来自百度百科。
physixfan
eaglefantasy
Eagle_Fantasy
宇宙的心弦
Traction Theme by The Theme Foundry
Copyright © 2025 physixfan. All rights reserved.  宇宙的心弦 by physixfan is licensed under a Creative Commons Attribution-NonCommercial-NoDerivatives 4.0 International License.
宇宙的心弦 by physixfan is licensed under a Creative Commons Attribution-NonCommercial-NoDerivatives 4.0 International License.
Necessary cookies are absolutely essential for the website to function properly. This category only includes cookies that ensures basic functionalities and security features of the website. These cookies do not store any personal information.
Any cookies that may not be particularly necessary for the website to function and is used specifically to collect user personal data via analytics, ads, other embedded contents are termed as non-necessary cookies. It is mandatory to procure user consent prior to running these cookies on your website.

我觉得,这里“可能性是均等的”应该提前指定。比如“先随机取一个端点,再随机取另一个”的话,就应该是1/3。
o(∩_∩)o…
澄清一点 我不是环球科学的编辑 是美国科学人的签约作者…
负责和国内的环球科学联系…囧
其实我也觉得循环定义了。
$$frac{1}{3}$$
一个圆的弦是其两个端点在圆上的线段。假定弦是在一个单位圆上随机画出的,问弦长超过√3的概率是多少?
我们的回答是这要决定于什么样的随机,反言之,选择什么坐标。样本空间Ω是圆上所有可能的弦。为了求弦的坐标,首先引入直角坐标系,其圆心在原点(图2.9)。注意到弦垂直于含有其中点的径向线。我们可以用下列给定来描述每个弦:
1 . 中点M的直角坐标(x,y), 或
2. 中点M的极坐标(r,θ), 或
3. 端点A和B的极坐标 (1,α) 和 (1,β) .
对于每种情况,我们认为随机是指:随机选择这些坐标。
我们用计算机模拟很容易估计这种概率。在编模拟程序时,进行某些简化会更方便些,依次叙述如下:
1. 为了模拟这种情况,我们从[-1,1]随机选出x,y值。然后检查是否 x^2+y^2≤1, 否则,点M(x,y)就会落到圆外去了,也就不可能作为弦的中点了,故应当舍去此点。如果检查合格,,即可作为弦之中点,其长按公式:
2. 为了模拟这种情况,可考虑因此圆任意旋转时,其弦长不变,故进一步假定弦处于水平状态。然后从[0,1]中随机选择r,则此中点极坐标为 ( r , π/2 )的弦之长按公式:
3. 为了模拟这种情况 ,可假定端点B之极坐标为(1,0)不变 【即r=1,β=0】,然后A点的极坐标α在[0,2π]区间内随机选择 ( r=1),利用余弦定理,此弦之弦长按公式:
程序BertrandsParadox就是进行这种模拟的。运行这个程序。产生的结果示于图2.10
图中第一个圆内画出了一个较小的圆。与此小圆相交的弦之长至少为√3。图中第二个圆内与图中竖线相交之弦其长至少为√3 。 第三个圆,也是竖线与其长大于或等于√3之弦相交。
对上述每种情况我们都做了大量次数的试验运算,并记录了弦长超过√3的次数比例。每隔第100次试验,打印一次结果,直至10000次。
观察到三种情况的次数比例之不同,颇为有趣。这决定于坐标之选择。这个现象第一次由贝特朗观察到,现在是大家知道的’贝特朗悖论’(Bertrand’s Paradox)。【3】
实际上,所谓“悖论”一点也不悖。这只是反映了选择不同的坐标会导致不同的概率分配这一事实。至于哪一个分配是“正确”的,决定于事先确定的模型的如何应用或阐释。
你可以想象一个实际试验包括抛掷麦秆到纸牌桌上画好的圆。“正确”的坐标指定不论圆画在桌面的哪个位置,或者牌桌放在房间的什么地方。Jaynes 4 曾经指出唯一符合要求的指派是(2)。在这个意义上,指派是自然的或“正确”的一个(见习题11)。
如果我们令√3为一个标记为等边三角形的边长,我们就很容易看出每种情况的真概率是什么。因此如果弦之中点到原点的距离d √3 (见图2.9)。
下列计算式确定每种情况中L>√3时的概率。
1.L > √3 ,如果(x,y)在半径为1/2的圆内,其发生的概率:
2.L > √3 ,如果 ;│r│ √3 ,如果:2π/3<α<4π/3, 其发生的概率:
由此可看出图2。10的模拟试验值非常吻合这三个理论值。
挺有道理的,不过图片都不见了。这是从哪个网站上贴过来的?
我认为第三点是有道理的。
第一种先固定了弦的方向,计算出来的结果没有考虑到每一个方向也是有概率的。
第二种也是一样,先固定弦的端点,可是端点可以是任意的啊,凭什么就要固定在这个点上来算概率呢。
第三种的正确性,我想不言自明吧,弦和它的中点一一对应,只要考虑中点的位置当然就足够了。
第一种正是认为取每一个方向概率相等,这个应该没什么问题吧
第二种也是,在圆周上随机取一个点,每个点被取到的概率是一样的
对啊,概率一样可是计算的时候也要算进去啊。
就像从{1,2}中任意取一个数,取到1或者2的概率一样,都是1/2,这个1/2一定要算进去,不能一样就算成1啊。
第一个应该算假等概率事件,有一个隐含的假设:通过单位长度的弦的个数期望(概率)是相等的,但是比较合理的假设应该是:圆周上任意两点都能连成一条弦,且都是等概率事件,这样的话,第一种解法取的事件是完整且唯一的(对称性),但是非等概率时间,所以还要乘以概率,即:弦长度要转化成对应的弧长——两端对应的弧长共为4π/3,中间这两段总长为2π-4π/3=2π/3,所以概率为1/3。
第二种取法较巧妙。
第三种取法的规则有些问题,如果按照反对称扩展后,肯有重复取叠加了的事件。
个人认为第三种较好。
第一种,你将弦的方向旋转半周不是会重复吗?
第一种的答案1/2其实包含了旋转一周的情况
而事实上你只能转半周,因此需除以2得1/4。
而第二种会出现同样的问题,你自己看一下。
而第三种因为选取不同的中点,且无穷多个,而不同的中点只一一对应唯一的一条弦,不会重复,也完备。
无穷的情况你不能用有限的观点来看。
对于第一种:
假如过直径作垂直的弦,那么三个部分可以做的弦条数之比是多少?1:2:1,对不?
那么换种方式看三个部分对应的半圆上的弧长之比是多少?1:1:1!
那么连接圆上两点的弦数量之比呢?1:1:1,对吗?
第二种:
我想的还不够成熟,暂且不谈。
第三种:
其解法的基本假设是没一个中点只对应唯一一条弦!
那么弦中点是圆心呢?多少?
无数条。
对应关系不统一?
第二种应该也是存在一定矛盾的。
三种算法应该都犯了同一种错误:
无限的东西用有限的观点而分割了!
我想主要是看你让弦长进行变化的时候依据什么参数进行调整吧。比如前两种算法,你的参数是弦心距或者是圆周角时,都可以列出相关的弦长方程,但是这样算出来的弦长变化是不一样的——如果我们都认为参数的变化是平均的,那么就可以把产生问题的原因称之为“等可能事件的定义不一致”~
联想到一个悖论:一个圆和一条与之相离的直线,谁的点更多。1.圆在直线上滚一周,圆上点遍历,直线多于圆。2.以圆心为起点作射线,无端点半圆上的点和直线一一对应,圆多于直线。3.以圆内另外的点为起点,又有不同的结果……
我只有高1 觉得你们想复杂了 第二个是对的 第一和第三都错了 而且犯了一样的错误 那就是在推论前先肯定了弦经过指定区域的概率和其他地方时相同的 这是不对的 至于每块地方的概率我就不献丑了
第一种是假定弦的中点在某直径上均匀分布。即在直线上取一点。
第二种是假定一端固定另一端在圆周上均匀分布。
即在圆周上取一点。
第三种是假定弦的中点在圆内均匀分布。
即在圆内取一点。
很明显三种取法完全不同。