音调无穷上升的音乐
终于看完了《哥德尔、埃舍尔、巴赫——集异璧之大成》，在最后一章有一个无穷升高的卡农让我回忆起以前貌似在Matrix67那里看过的一个东西，就是一个段音乐貌似音调一直在升高然而当你循环播放的时候发现还是总是在升高…
这个音乐放在这里让大家下载听一听。
感觉挺神奇的，这种音乐有个学名叫做Shepard tone（谢泼德音调?），维基百科有介绍见这里。《GEB》这本书上有个配图解释了为什么会是这个样子。
上图中大小表示音的强弱，看着确实是这么回事。音调最高的那一行音越来越弱，直到消失的时候最低的音逐渐从无到有逐渐加强并且升高…而且衔接处是听不出来有音调的突变的…
听着这种音乐，让人不得不联想起埃舍尔的画，一对比就会发现其实这种音乐和下面的画是一种同构：…
圆的弦比内接正三角形之边大的概率是多少？
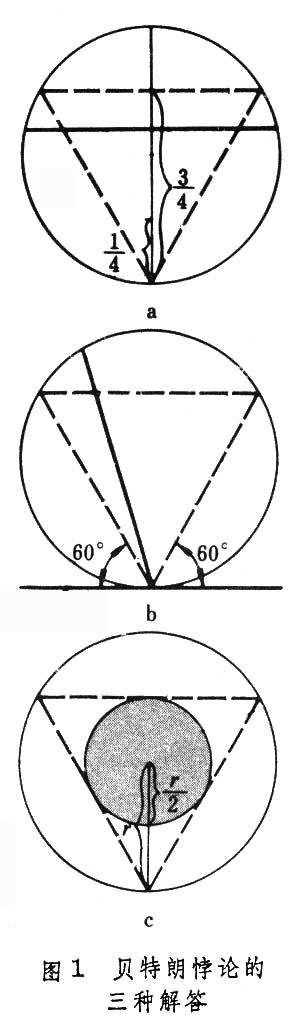圆的弦比内接正三角形之边大的概率是多少？
偶然间从庞加莱（Poincaré）（又被翻译成彭加勒）的《科学与假设》的概率演算这一章看到了这个命题，他最早由贝特朗提出，故又叫做贝特朗悖论。这一问题有三种解答，答案分别是1/2、1/3和1/4，我怎么也想不清楚到底哪一种是对的，其他的为什么错了，请路过的大牛们帮忙看一看。
解法一：由于对称性，可预先指定弦的方向。作垂直于此方向的直径，只有交直径于1/4 点与 3/4 点间的弦，其长才大于内接正三角形边长。所有交点是等可能的,则所求概率为1/2 。
解法二：由于对称性，可预先固定弦的一端。仅当弦与过此端点的切线的交角在60°～ 120° 之间，其长才合乎要求。所有方向是等可能的，则所求概率为1/3 。
解法三：弦被其中点位置唯一确定。只有当弦的中点落在半径缩小了一半的同心圆内，其长才合乎要求。中点位置都是等可能的,则所求概率为1/4。
这个问题的答案到底应该是多少呢？
顺便说一下，《科学与假设》里有一个观点我很认同，他觉得古典概型中概率的定义不严谨。定义：“若只有有限个不同的基本事件，且每个基本事件发生的可能性是均等的，则事件A的概率等于事件A包含的基本事件数除以基本事件总数。”可是，定义中出现的“可能性是均等的”如何判断？这是不是用概率来定义概率了？这样的定义不算循环定义么？
注：文中的三种解法及图片来自百度百科。…
一个关于级数的疑问
大家应该很熟悉ln2的级数展开吧：
ln2=1-1/2+1/3-1/4+1/5-1/6+1/7-1/8+……①
把①两边每一项乘以1/2得到：
1/2*ln2= 1/2 -1/4 +1/6 -1/8+……②
上面②的数字间距比较大仅仅是为了与①的相关数字对齐。把①②相加，按照纵列结合各项，于是我们得到
3/2*ln2=1+1/3-1/2+1/5+1/7-1/4+1/9+1/11-1/6+……③
我们惊奇地发现，③的右边仅仅通过顺序的变换就可以得到①的右边，但左边却确确实实的不相等！难道无穷级数不支持交换顺序的运算？
有的人马上举出1-1+1-1+1-1+……这个著名发散级数跟我说无穷级数肯定不能交换顺序，可是一定要明确①和③两边是收敛的阿！收敛就决定了这不是个太小儿科的问题。
到底是从①变到③的某个过程不被允许，还是连收敛级数也真的不能交换顺序？我期待有谁能给我个令我信服的答案。
update:最近看了一些书和文章似乎对此问题有些明白了，感谢网友们的帮助！…
有趣的堵火车悖论
当年爱因斯坦(Albert Einstein)提出令人费解的狭义相对论之后，有很多人提出了各种各样的悖论，例如孪生子悖论，在例如今天我要说的堵火车悖论（这个名字是我自己叫的，不知道其他人叫它什么）。这个问题是这个样子的：
未来的某一天，科技高度发达，火车行进速度飞快，足以产生明显的相对论效应，人们也都精通相对论知识。一天，两个盗贼得知有一列载满富翁的火车将通过他们的地盘：一个中间有隧道的山坡，火车将从隧道穿过。已知隧道的长度恰好和火车静止时的长度相等。两个盗贼这样盘算：根据动尺缩短效应，我以我自己为参考系，火车将相对于我高度运动，长度将变短，因此我们可以两个人分别站在隧道的一段，等到火车车身完全在隧道内的时候，两人同时用一块石头堵住隧道两端，把火车封在里面，这样就可以下去抢财物了。富翁们不知从那里得知了倒贼要行动的消息，哈哈大笑，想到：他们不可能成功，根据动尺缩短效应，我以我在的火车为参考系，是山和隧道在高速运动，缩短的应该是隧道，因此我们的火车不可能在某个时刻完全处于隧道内而被封在里面。看来，他们两方说的都有道理，那么问题是：火车究竟能不能被封在隧道内呢？…
机械能守恒需要特殊参考系么？
一个从静止（相对于地面静止，将地面称作S系）开始自由落体的物体满足机械能守恒这是大家闭着眼睛都知道的事情，可是一天我突然想到了一个问题。如果我们换一个参考系，假如说我乘坐着一个电梯，以10m/s的速度（相对于大地）匀速下降，以我为参考系（称作S’系）来看前面这个自由落体的物体，机械能还守恒么？考虑到1秒的时候，物体相对于地面的速度也恰好是10m/s，我们不妨以0到1秒这段时间的状态来研究。一开始0秒的时候，物体相对我（S’系）有10m/s的向上的速度，势能是mgh。在1s钟这个时刻，相对于S’系物体静止了，即动能为零，而高度减小了，即势能也减小了，这样看来机械能不就不守恒了？！
这可能么？一个物理过程，以地球为参考系，机械能就守恒，而换一个相对它匀速运动的新参考系，机械能却不守恒了？强烈的物理思想告诉我，宇宙中不存在特殊参考系，能量守恒在任一惯性系中都一定是成立的。既然地球近似的看成惯性系机械能守恒了，那S’系没有任何理由违反机械能守恒！
问题出在哪里呢？对这个问题，我苦苦思索了两天，终于在一天睡觉的时候悟出来了。原来，问题就出在地球这个“近似”的惯性系上。虽然地球质量极大，在处理一般问题的时候可以认为是很好的惯性系，可是就在现在这个小问题上这个近似出现问题了。请听我慢慢讲解。…
