有趣的无规行走模型
昨天和一帮子同学出去玩,晚饭时间点完菜等待上菜的时候有两个同学玩起了一个非常无聊的游戏:甲同学扔硬币,乙同学猜正反面,如果乙猜对了则乙的鼻子变长1cm,反之如果乙猜错了则鼻子缩短1cm。(这个是和谐过的版本,原始版本变长变短的不是鼻子而是另一个猥琐的东西…)。他们正在无聊的玩,全然不知道这么玩下去他鼻子长度的绝对值期望是多少…其实,这正是我高一的时候在费恩曼物理学讲义上看到的一个数学模型:Random Walk(无规行走)。对于这个模型,我敢说绝大多数人凭直觉会觉得鼻子长度的绝对值最终的期望值会是0,但事实绝非如此,你可以自己扔几次硬币试试,正确的答案应该是你扔硬币次数N的平方根!
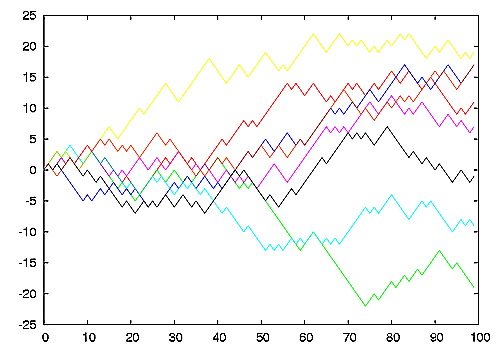
下面给出证明,该证明基本来自《费恩曼物理学讲义》第一卷:
为了证明看起来舒服一些,还是用最原始的模型吧:我站在一个坐标轴上,前为正方向,抛掷一枚硬币,如果正面朝上则我向前走1m,如果反面朝上则我后退1m,在我抛掷硬币次数N足够大的时候,求证我离远点距离的期望值是根号N。
离原点的距离,我们需要一个绝对值来表示,我们设为|D|。为了表示清楚在投掷了N次硬币之后的距离,我们为D加一个下标,可惜网页上显示下标比较麻烦,我就这样表示吧:|D(N)|。可是在这里,用另一种量度进度的方法更为简便,这就是用距离的平方D(N)^2来表示,因为D(N)无论正负D(N)^2总是正的。在这里为了区别开期望值与真实值的区别,我们用<D(N)^2>来表示期望,而D(N)^2表示真实值。
当N=1的时候,毫无疑问D(1)^2=1。
当N>1的时候,D(N)^2的预期值可以从D(N-1)求得。如果走了N-1步以后,我们得到D(N-1),那么经过N步后,就有D(N)=D(N-1)+1或者D(N)=D(N-1)-1。其平方为:
D(N)^2=D(N-1)^2+2D(N-1)+1或者D(N)^2=D(N-1)^2-2D(N-1)+1
对于大量的无规行走,我们的平均预期值恰好是这两个可能值的平均值。于是D(N)^2的预期值就是D(N-1)^2+1。一般而言,我们对D(N-1)^2所应期望的预期值根据定义就是<D(N-1)^2>,所以
<D(N)^2>=<D(N-1)^2>+1
之前已经说明了<D(1)^2>=1,所以归纳一下就可以得到<D(N)^2>=N。。。!
把上面的式子开平方就可以得到我们要证明的漂亮结果|D(N)|=√N。
话题再回到昨天的游戏上面,他们当然以为最终的某物长度期望值为0,实际上长度为正负根号N。如果是正的就让乙同学给赚了,如果是负的,嘿嘿…



了解了。。可是怎么直觉地理解这个结论呢?
怎么直观理解这个我也不清楚…还是理解不够深刻…
原来改版了~
话说我也正证过…
同时matrix67提到过如果是上下左右四个方向,那么距离的期望就好求很多……
我怎么没有印象Matrix67神牛还写过这个问题?看来我记忆力严重衰退了..
他写的是二维上的……http://www.matrix67.com/blog/archives/959
看来Matrix67神牛的旧文章还是得时常去拜读一下的..
关于这个宇宙最让人难以理解的地方就是她竟然是可以被理解的。
改版了。
貌似改版好长时间了..看来是我好长时间不写东西了大家来的少了..
哦 我也做过类似的问题,移动距离不是+-1,而是一个正态分布,结果也是正比于根号n
另外对于三维的情况也是正比于根号n
嗯 这个在费恩曼物理学讲义上也都有 这就是布朗运动的模型
它们共同点是位置的增量独立且服从同分布…
若设n时刻位置为Yn,,Y0=0,增量Xn=Yn-Y(n-1)
则
E|Yn|=E|∑Xi|
=( D(∑Xi) )^0.5
=(∑DXi)^0.5
=(nDX1)^0.5
什么猥琐东西?
并且怎么让东西缩短呢 – -?
这个猥琐东西..如果猜不到还是不知道为好…
我说我猜到了……
这个很久前某人跟我说过.当时是如果正面(他)就去追女生.反面就不去.然后他说数学的直觉告诉我必须要出手了…
大牛鼻子这个词和谐的好!
小小乐一开始不就是以为势是鼻子的意思吗..哈哈
其实是你偷换了概念。
最终长度的期望依然是0,但是长度平方的期望是N,这是两回事情。
=N是不能得到|D(N)|=√N的
我也注意到了 所以我一直用的词是“他鼻子长度的绝对值” 如果不加绝对值 期望确实应该是0
就算是绝对值,也不可能是根号N
比较一下绝对值期望和平方期望的公式就看出来了
绝对值期望应该会小于根号N
如果只是要说明期望不是零,用树状图就可以了。考察走了N步后的树状图,对每个分支的结果(当然是正值)求平均就是N步后距离的期望值,这当然是正数。
你的这个证明里有些细节好像不太对,有些地方最好明确一下。物理学家玩数学经常不注意确定一些基本的问题。比如考虑拓扑问题时不注意拓扑的选取,考虑概率问题时不注意样本空间的选取。。。
嗯..物理学家玩数学经常不注意确定一些基本的问题。说的挺对..一般物理书上的证明都不太注意严格性…
绝对值的期望….估计没有人会认为是0吧….
以我高一的时候那智商就以为是0呢..
最后那句话有点问题,拿大牛的势为例,玩这个游戏n次后,不能说原长度是0,玩完就成了正负根n了,结合正态分布曲线的图像,应该这样表述这个概念:大牛的势长极其有可能依旧桎梏于正负根n之间
仔细想了好久,终于差不多明白这个解法错在哪里了。
首先,期望值是一个统计值的唯一值,当文中提到:
就有D(N)=D(N-1)+1或者D(N)=D(N-1)-1。
期望值不能得出这样的公式,正确的共识是:假设前N次投币后的长度为S(N),那么从N-1次到第N次有两种可能,各是50%的概率,也就是S(N)=S(N-1)+1或者S(N)=S(N-1)-1。
D(S(N))=0.5*(D(S(N-1)+D(1))+0.5*(D(S(N-1)-D(1))=D(S(N-1))
所以进行N次试验的均值和进行N-1次试验的均值一样。请注意,我上面公式的推导,运用的是D(f1(x)+f2(x))=D(f1(x))+D(f2(x)),这个公式的正确性是可以证明的。
而文中使用的公式:D(N)=D(N-1)+1或者D(N)=D(N-1)-1,本身就是错误的,因为均值只是一个统计值,是唯一的,但是得出了两个解。文中把一次试验的统计值和均值的概念混淆,从而得出了错误的公式和错误的结果。
另外补充一下,我们学习的很多教科书,偏向于介绍公式的运用,而忽略对问题本源的探求。例如:很少涉及问题的假设,问题解法的具体意义,或者解法的适用范围。
于是让我们产生了一些似是而非的错误解法或者公式。例如本文将均值的概念和一次试验结果的值混为一谈,从而得出了看似正确的公式和奇怪的结果。
刚才看了他人的回帖,如果我们求的是绝对值得均值,也就是D(|S(N)|),那么一个直接的解法是:
D(|S(N)|)=2^(-N)( C(N,0)*|N-0*2| + C(N,1)*|N-1*2|+…+ C(N,N)*|N-N*2| ).
可以解得
D(|S(1)|)=1
D(|S(2)|)=1
D(|S(3)|)=3/2
还是再重复一下,这里的关键在于将一次实验的结果S(N)和f(x)的均值D(f(x))用不同的符号表示,而不要混为一谈。
开始把我吓了一跳以为我这么挫呢,其实这个问题的答案的平均值应该是0,方差才是你正负sqrt(N);你是个好小伙,我都26了加油,你的博客很好!
同意fennec
对于任意N,可能的行走路线数总是有限的整数,对每种可能的路线的距离值进行平均不可能得到无理数。
另外,“在我抛掷硬币次数N足够大的时候”,这句话没看出来有什么用。
对于任意N,可能的行走路线数总是有限的整数,对每种可能的路线的距离值进行平均不可能得到无理数。
=================
cannot agree more.
这句话也错了,”于是D(N)^2的预期值就是D(N-1)^2+1″, 这个”于是”得的比较突兀。 没有任何理由。 由(A+B)/2=C, 不可以说 (A^2+B^2)/2=C^2.
=N正确,但是=√N错了。方均根值通常不等于期望值。
你的博客很不错,关注…
我和Duanzheng是类似的情况,费曼讲义6-3确实翻译的不很数学,不过我是高二的学生哈,学哥们好啊
你给出的证明看起来似乎是对的但对于该证明我有两个困惑1.期望值的意义 比如在该实验中 第一次前进二次后退第三次前进…….为何不是期望的情况 如果这样期望值为02.对于根据两种情形下的递推公式直接相加再除2求均值的方法 看似简洁 但这样做真的可以吗 我找不到理论或经验上的依据 并且那种结果为0的方法 似乎也没有致命的错误
《平均预期值恰好是这两个可能值的平均值》,请问这怎么理解呢
正数序列也能收敛到零的
有理数序列是能收敛到无理数的
这个地方我也有很多地方不明白,我带入进去实际算了下,我觉得当N=1时,D的取值有2中情况,取值是+1和-1,绝对值的平均数为1,但当N为2的时候,有4种情况,+2,0,0,-2,这时绝对值的平均数就是(2+2)/4=1.当N为3时,D的取值为3,1,1,-1,1,-1,-1,-3,这时的绝对值平均数为12/8=1.5,和书上的结论差别很大啊,按书上的结论应该是1,√2,√3才对啊。我不知道我错在哪里了
我看了你们的评论,更迷惑,=N是不能得到|D(N)|=√N的?我也觉得 由(A+B)/2=C, 不可以说 (A^2+B^2)/2=C^2.难道书中是错的?
但很多书上都是文中的解释,我觉得应该是我们什么地方理解错了吧
为什么不用D的2m次方,而用二次方?
%%
My site Cbd jelly hash