最小作用量原理与物理之美3——牛顿力学
就像最小作用量原理可以推导出所有几何光学定律一样,力学中也存在一个最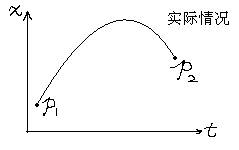 小作用量原理的特例可以推导出整个牛顿力学。今天我们就来研究研究这个。
小作用量原理的特例可以推导出整个牛顿力学。今天我们就来研究研究这个。
有这样一个事实:假定有一个质点在引力场中通过自由运动从某处移动至另一处——你把它抛出去,他就会上升又落下。如果画出x-t图(为了简化,只考虑一维的运动,设x轴是竖直的轴),那么运动图像是一条抛物线。你可以尝试着通过起点和终点画一些别的曲线,如果计算出经历整条路径期间动能减重力势能对时间的积分,你会发现所获得的数值比实际运动所获得的要大。如果我们设作用量S为
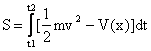
那么上面的事实换句话说就是作用量 S在实际运动中取得最小值。对上面字母的解释:t1、t2表示运动的起点和终点时刻,1/2*m*v^2是研究物体的动能,V(x)是其势能(这里把它写成是随x变化的函数)。当物体只受重力的时候,V(x)=mgx。我们在上一篇文章中说过,一个泛函取得极值可以令其变分等于0,所以在力学中,最小作用量原理的特例就写作:
S在实际运动中取得最小值。对上面字母的解释:t1、t2表示运动的起点和终点时刻,1/2*m*v^2是研究物体的动能,V(x)是其势能(这里把它写成是随x变化的函数)。当物体只受重力的时候,V(x)=mgx。我们在上一篇文章中说过,一个泛函取得极值可以令其变分等于0,所以在力学中,最小作用量原理的特例就写作:
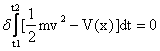
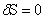
我们可以先定性的理解实际情况确实作用量最小。X增大时势能是增大的,作用量中势能前有个负号,所以应该在x比较大的时候多呆一段时间,而x比较小的地方尽可能快地往上爬,以保证动能减势能之差对时间累积之后尽可能小。
下面我想用基本的微积分变一个惊人的魔术:从最小作用量原理推导出牛顿第二定律F=ma!
我没完整学过变分法,因此我将主要根据《费恩曼物理学讲义 第二卷》第19章的内容,不直接用变分法而用高中生就能接受的初等的微积分来推导。
我们现在想要求的是一个泛函S的极值[之所以说S是泛函是因为,S的自变量是x随时间变化这个函数x(t)],可以类比当初学导数的过程。先回忆一下我们还没学求导公式的时候是怎么求导的:要求一个函数的极值,我们可以令x有一个无穷小的变化Δx,代入函数的表达之后运算并舍掉高阶无穷小量最后算出Δy,令导数等于Δy/Δx等于0即可求得y在何时取得极值。我们将模仿上述过程求泛函S的极值。
先进行一些前期工作。首先把v换掉,根据v是x对t的导数得到
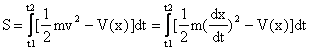
在下面的推导中,为了方便有时把x(t)简写作x。我们称真实路径为x0(t),而x(t)则表示某条假想的尝试路径。我们设真实路径与实际路径有一微小差别(当作小量)记作η(t)。同样为了方便有时把η(t)简写作η。因为我们的数学模型规定了p1、p2是空间中两个固定点,因此有η(t1)=0,η(t2)=0(这个规定是必须的,否则得不到任何有价值的东西)。
有了上面这些东西,我们开始对S进行运算。
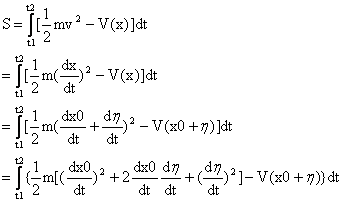
忽略掉高阶无穷小,即含有η^2或更高次幂的项,得到
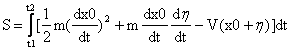
下面对V(x0+η)变形,如果知道泰勒级数的人可以容易的理解V(x0+η)如何展开,如果不知道的话也不要紧,类比导数(类比导数是多么重要啊!!!)。我们知道y可以写作y=y0+Δy=y0+y’*Δx,其中y表示y对x的导数。那个η和Δx地位是相当的,V(x)和y地位是相当的,类比着我们可以写出
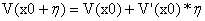
其中V’表示V的导数。所以
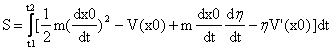
还记得δS的定义吧,它就是我们的尝试路径得到的S减去实际路径得到的S0。所以
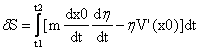
现在的问题是,这里是某个积分,虽然我们还不知道x0是什么,但是我确实知道不管η是什么,这一积分必须恒为零。我们需要做的是把积分号里面那部分写成η乘以某个东西,如果这个东西恒为零了,那么整个积分式就恒为零。
所以我们想用所谓的分部积分对S进行变形。分部积分可以从导数的乘法公式得来,假设我们有某个函数f(以t为自变量),我们想求f*η对t的导数,则有
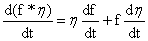
两边同时积分得到

上面的式子就叫做分部积分。令上式的f=m*dx0/dt可以得到

来看上式的第一项,因为前面说过的,η(t1)=0,η(t2)=0,所以第一项等于零!所以
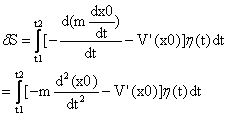
我们终于得到了想要的结果——某个东西乘以η(t)总等于0!那就令这个东西恒等于零好了!看看这是什么?
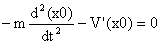
第一项中x0对t的二阶导数正是加速度a,第二项中势能V(x0)的导数,不正是-F么!!!上面那个式子其实就是F=ma!!!
好了,花了这么大的力气终于从最小作用量原理推导出了牛顿第二定律,从而基本上可以解决任何经典力学问题了。在《最小作用量原理与物理之美2——自然中无处不在的极值》中我举了重力势能最低、表面势能最低的例子,这其实就是作用量中动能那一项恒等于零的结果。需要注意的是,尽管我们总是叫最小作用量原理,实际上作用量不一定最小,它可以是极小值、极大值或者恒定值,重力势能最低实际上是作用量取极大值的情况(作用量中势能前有个负号)。
有了这个力学的最小作用量原理,我们只要把合适的V(x)带进去就可以得到各种各样的结果,很多东西就能被理解了。有人会说牛顿力学不是错的么,相对论更准确,从最小作用量原理推出的是不准确的结果,那么它本身也不会正确。我想说的是,原理本身没有错,主要是我们的推导没有考虑任何相对论效应,作用量本身也没有经过相对论的修正,但是严谨的表述是可以实现的。



It’s very interesting!
动能+势能=常数,你把这个带到第一个公式里,会发现对(动能 – 势能)路径积分没什么意义。积分目标函数中只要动势能其中一个就能导出f=ma,换句话说f=ma是蕴含在动、势能的定义和守恒定律里的,楼主的作用量没有显得更本质
感谢博主!
吓到了
高三的时候就这么厉害…高一小学弟表示吓到了