细推物理须行乐 何用浮名绊此身
Search
-
Recent Posts
Random Posts
Tags
Links
有一个经典问题:8*8的棋盘,去掉了左下角和右上角2个格子,请问能否用31块1*2的骨牌覆盖整个棋盘。这个问题的答案应该人人都知道吧,染色之后一目了然。
那么,有人要问了:如果去掉的是1红1白的格子各一个,结果是怎样的呢?比如下面的这个图:
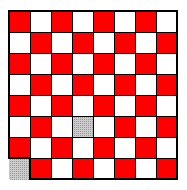
你可以自己画几个图试一试。你能证明一定可以覆盖?还是可以给出反例呢?
据说,这个问题刚出来的时候,通过复杂的理论,终于得到了证明。也就是只要在这个图中去掉一红一白两格,肯定可以被覆盖。
这里,我们将看到一个复杂的问题怎么通过一个简单的方法来证明。我们接下来不但要证明可以覆盖,而且要给出覆盖的方法。看到这里你可能会想到了:构造——对了,只要构造了一组解,原问题便解决了。
我们把原来的棋盘按照下图所示的方法剪开:(沿着绿线):
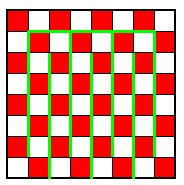
我们就把这个棋盘变成了一个环。注意到整个环都是红白相间的。假设我们从图中去掉一个红色格子,再去掉一个白色格子。我们就得到两条链:每一条链都是红色->白色->红色…->白色。这样我们只要沿着链每次的两个格子放即可(注意到相连的两个格子不存在和骨牌形状不同的情况:1*2,你能找出第二种形状吗?)。把两条链放完,这个棋盘就被覆盖满了,我们的问题也就解决了。
文章来自:http://evalls.yo2.cn/articles/%e8%af%81%e6%98%8e%e7%9a%84%e7%bb%9d%e5%a6%99.html
physixfan
eaglefantasy
Eagle_Fantasy
宇宙的心弦
Traction Theme by The Theme Foundry
Copyright © 2025 physixfan. All rights reserved.  宇宙的心弦 by physixfan is licensed under a Creative Commons Attribution-NonCommercial-NoDerivatives 4.0 International License.
宇宙的心弦 by physixfan is licensed under a Creative Commons Attribution-NonCommercial-NoDerivatives 4.0 International License.
Necessary cookies are absolutely essential for the website to function properly. This category only includes cookies that ensures basic functionalities and security features of the website. These cookies do not store any personal information.
Any cookies that may not be particularly necessary for the website to function and is used specifically to collect user personal data via analytics, ads, other embedded contents are termed as non-necessary cookies. It is mandatory to procure user consent prior to running these cookies on your website.

是不是可以直接匹配做一下。
听不懂…
非常牛的思想啊,把复杂的二维情况化为简单的一位情况,真有想象力。