钝角其实和直角相等!我们的教科书真实率低于5%,连数学也不例外。
“我们的教科书真实率低于5%,连数学也不例外,年轻人要敢于怀疑。越是从小学习,看起来理所当然的知识越值得怀疑。钝角其实等于直……”1968年冬天,在刺骨的寒风中,数学教授赵文武凛然站在后海的岸边,最后一句尚未说完,便被疯狂的红卫兵挂上石头沉入了后海。
在我们的少年时代,有很多人都有这样的经历,在各种平面几何问题中抓耳挠腮,证明来证明去,为了证明一个角是直角而浪费了精力,荒废了青春。很多人因为不会证明平面几何中关于直角的问题,遭到父母的毒打,乃至与梦中的重点中学、大学失之交臂。可又有多少人知道,其实钝角就等于直角。所有钝角尽管看起来不一样大,但是早在欧几里得时代,伟大的古希腊数学家们就早已通过严格的数学证明了钝角统统等于直角!可是在中国,黑暗的中国教育界却可耻的隐藏了这一秘密,当今中国几乎就没有人知道钝角和直角相等这一本该人尽皆知的秘密!
众所周知,平面几何的最经典著作当属欧几里得的《几何原本》,当今所有的平面几何课本都基本按照原本的框架讲述。而关于钝角等于直角的证明,其实就静悄悄的隐藏在《几何原本》的后记当中。下面贴出古希腊数学家给出的证明:
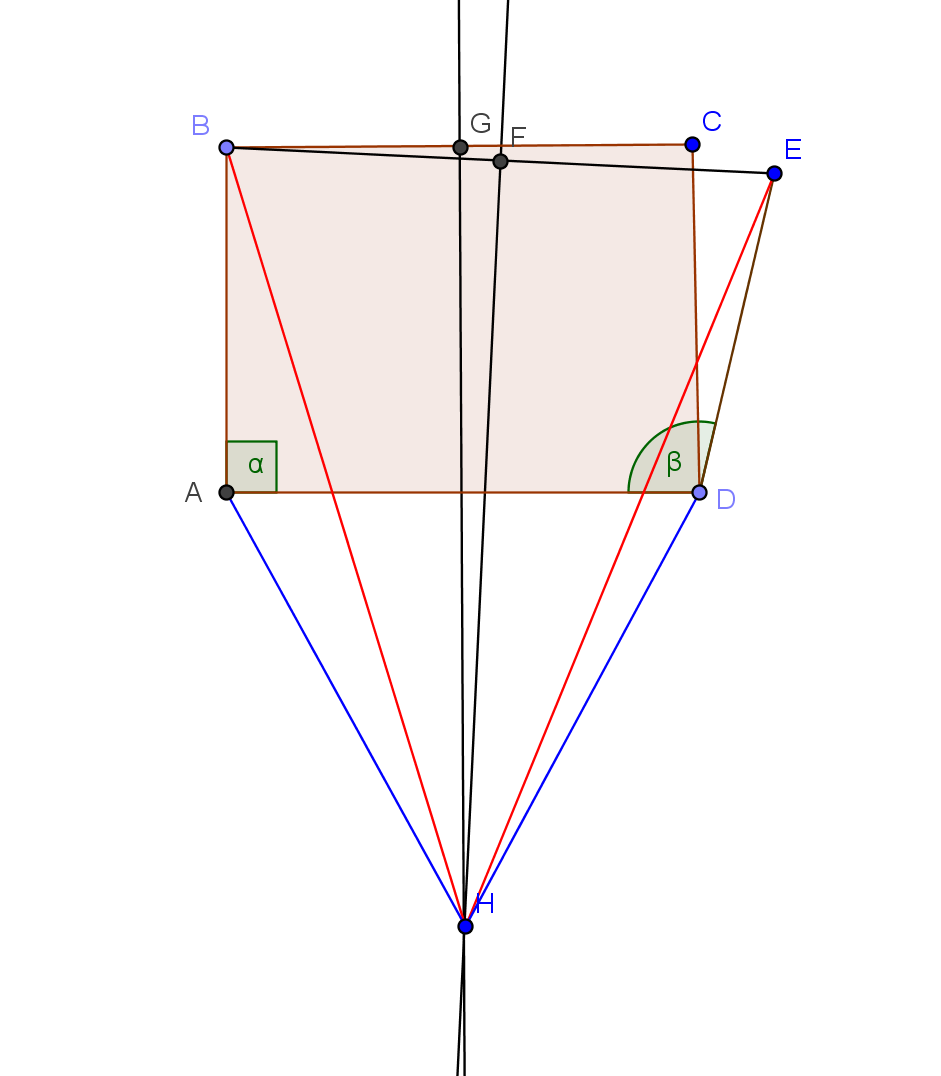
如上图,ABCD为矩形,在矩形外选取一点E,使得DC=DE。G、F分别为BC、BE中点,然后过G、F分别作垂线,两条垂线相交于H。连接H与ABDE四点,就形成了上图。(为了让证明过程更清晰,已经把一些相等的线段染成了同一种颜色。)(因为种种原因,图可能画的有点不太准确有点难看,请原谅。。)
现在开始伟大的证明:
因H在AD的垂直平分线上,故AH=DH。因H在BE的垂直平分上,故BH=EH。因DC=DE且ABCD为矩形,故AB=DE。至此,ΔABH和ΔDEH的三边都相等,根据“边边边”(初中平面几何里学的全等三角形判定条件之一),ΔABH与ΔDEH全等。因此∠BAH=∠EDH。上式两边分别减去∠HAD和∠HDA(因等腰三角形,这二角显然相等),则可得出图中α、β二角相等!显然,α为直角,而β为钝角!
因此可以得出我们的结论:所有钝角等于直角!
从古到今,几乎所有国家的数学书上都白纸黑字的写着钝角等于直角。1949年新中国成立后,所有数学课本上则明确区分了钝角和直角。同时,所有民国时期的数学课本均被销毁。这样做的真实目的,是为了让小学生初中生在数学的苦海中挣扎,让他们把自己的全部精力耗尽于证明各种直角相关的平面几何题,这样他们便不会有精力心生叛逆上街游行闹事。
对平面几何被如此猖狂的扭曲,大多数中国人选择了失忆和沉默,只有一个人站了出来。
赵文武,1909年6月31日生于广州,1928-1936年就读于南京国立中央大学数学系。年少时即表现出天才般的数学造诣,其博士论文《11维欧几里得空间中的直角与钝角的大小关系》引起国内外数学界的震惊。吴与同一时期在清华大学暂露头角的华罗庚一起被认为是中国数学界的两大青年才俊,并称“南赵北华”。两人成为惺惺相惜的挚友。建国后,华罗庚内敛、现实的性格使他在历次运动中采取了随波逐流、明哲保身的无奈态度。而赵文武固执地遵循着在民国故都接受的道德教化,使他保留了坚持真理、敢怒敢言、不向任何威权妥协的君子遗风。50年代末,赵文武无法接受所有数学课本上不把钝角与直角等同的做法,坚持传授所有钝角等于直角的秘密,在反右运动中被打倒。同样在历经打击后,华罗庚忍辱负重,违心地附和“数学要为工农兵的实际生产服务”,并多次暗示吴妥协,“留得青山在”,赵文武却毫不动摇,继续坚持着钝角直角相等。最后,在文革中,不明真相的红卫兵被煽动起来,将赵文武插上“反革命学术异端”的牌子,游街批斗后沉塘。在挂上了石头,被推下后海的最后一刻,赵文武面对已经失去理智的红卫兵,仍然从容地说:“我们的教科书真实率低于5%,连数学也不例外,你们年轻人要敢于怀疑。越是从小学习,看起来理所当然的知识越值得怀疑。越早让你们学,越是有人迫切地希望你们在没有辨别能力的时候学进去。因为你们大了就不那么好骗了。所有的钝角,都是等于直角的。。”在一片“打倒反革命疯子赵文武!”的喊声中,赵文武被扔进了水中。
在那个人人自危的年代,华罗庚强忍着心中的悲痛,一直不敢公开表达对赵文武的悼念之情。1978年赵文武被平反,华罗庚第一个来到赵的墓前。他的眼泪像断了线的珠子一样不停地流,“文武兄,我来晚了……”
赵文武之后,中国再没有人敢公开支持钝角等于直角。后来也曾有民间团体将上面的证明用图整合到徽标上,希望籍此暗语提醒世人“钝角等于直角”的事实。甚至通过自残等乖张怪异的举动吸引注意,未料无人知其苦心,意图却被官方首先识破,不得不流落异乡。从此,钝角等于直角的秘密也就渐渐不为人知了。
/************************我是蛋疼的分割线*************************/
写这篇文章的动机,是因为看到了人人网上的一篇神文《圆周率真的等于3.14吗?我们的教科书真实率低于5%,连数学也不例外。》, 读罢便深深膜拜作者的功力之深厚,我辈望尘莫及。原来一个经典数学伪证,经过这样一包装,可以如此吸引眼球传播广泛。于是我便不厚道的大段模仿原作,尝试着推广本文所述的经典伪证,同时验证一下是否真的只要经过包装数学问题都能引起大众注意。这个网站的读者也许大部分都看过这个经典伪证,但是我仍然为想不通它错在哪的读者提供一个线索吧:其实如果严格作图,H点应该更加靠下,以至于EH会跑到D点右侧,而不是上图中的那样,自己动手画出准确图形就自然可以看出这个伪证错在哪里了。



这不就是钓鱼文嘛?
每次在阅读器里看见这篇文章又变成了“新内容”,我就知道博主又在改文章了…
其实我没改文章。。我也搞不懂为什么阅读器里总是会把文章弹出来两次= =…
严格的说,这是欧几里德的公里系统有问题。证明本来就不应该依靠图形,而只依靠公理,而欧式的公理没有那么精确,可以推导像这种一个点在一条边的哪一侧。希尔伯特的公理系统可以解决这一问题。
这个证明有多个版本,我高中时看到的版本据说是苏格拉底为难一个骄傲的几何学家出的“鬼题”,当时我问我的老师,他们比较谨慎,用计算机画那个“图”,结果发现这个图本身是不存在的,也就是说几何学家被蒙了
做一个极端的例子很容易就可以证伪。让angle CDE 为90度就好了。可以推测HE应该在DE的右侧。
还以为交点会在矩形内- –
没看下面还以为是文章出错。原来是明知故犯。
并多次暗示
吴赵妥协= =,傻逼
逆证一下就知道错了
根本就不对。。。
为什么我很快就明白了……E点其实和B点重合的,用圆规来画也知道E点位置不对(有点低了)
我才发现这篇大作原来是大学长写的~~
sb的是你
是图画的不标准