复数方法巧解平面几何题

快放假了才买到《复分析——可视化方法》这本书，相见恨晚啊，这本神书，如果我能早点读，这学期的复变函数估计就学的不会这么吃力了。。。在这本书开头的地方有一个用复数方法解决平面几何问题的例子，我一看便惊了：这正是我初中时候见到的一道印象极其深刻的平面几何题，曾为它绞尽脑汁也没有想出做法呢，然而这本书就用复数的方法巧妙而自然给解决了~ 贴出来共享一下。

题是这样的：证明，在任意四边形的四条边上各做一个正方形，那么连接相对的正方形中心的线段互相垂直并且等长。示意图如下。

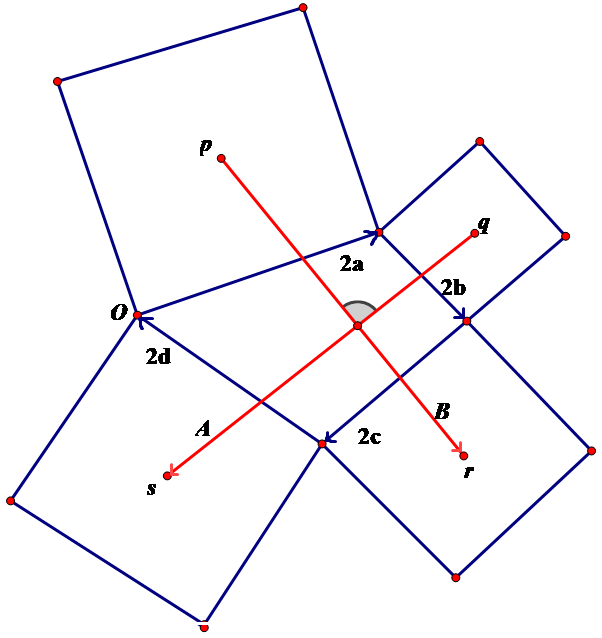
这道题的平面几何做法我已然忘却，现在的脑子也已经解不动平面几何题了。。就直接把书上的巧妙复数解法贴过来吧~

设2a、2b、2c、2d为表示四边形4边的复数（引入因子2只是为了方便），唯一的条件是这个四边形是闭合的，即a+b+c+d=0。

如果以图中O为原点，要想走到2a这条边的正方形中心，就要先走一个a，再沿着与a成直角（逆时针）的方向走过同样地距离。这样，由于ia正是a以逆时针方向旋转一个直角而得（想想复数乘法的几何意义，模相乘而辐角相加），所以p=(1+i)a。

同理，q=2a+(1+i)b，r=2a+2b+(1+i)c，s=2a+2b+2c+(1+i)d。

所以由q到s的复数A=s-q和由p到r的复数B=r-q就是 A=(b+2c+d)+i(d-b)，B=(a+2b+c)+i(c-a)。

我们想要证明的是A和B垂直并且等长，而这两个命题恰好可以由一个复数命题来表达：B=iA，即A+iB=0。这里仍然是用到了复数乘法的几何意义。

而这样一来问题就归结为简单的复数运算了：A+iB=(a+b+c+d)+i(a+b+c+d)=0。

问题轻松解决！

因为我高中就没有学过数学竞赛，所以不了解用复数解平面几何题是不是属于常规解法之一，反正我看到这个解法之后还是相当震撼的。《复分析——可视化方法》这本书才刚刚开始看，就已经惊喜连连。这本书的作者坚持认为，应当用形象化的东西来帮助我们学复分析，而不是用那套我看着发晕的形式化语言，相当符合我的风味，复分析本来该是最美的数学分支，却被我们的老师搞的就成了背公式算题。并且他还宣称是继承了牛顿那套用几何方法推演微积分的方法，等我继续看下去看有没有什么更加震撼的东西再来分享吧~