复数方法巧解平面几何题
快放假了才买到《复分析——可视化方法》这本书,相见恨晚啊,这本神书,如果我能早点读,这学期的复变函数估计就学的不会这么吃力了。。。在这本书开头的地方有一个用复数方法解决平面几何问题的例子,我一看便惊了:这正是我初中时候见到的一道印象极其深刻的平面几何题,曾为它绞尽脑汁也没有想出做法呢,然而这本书就用复数的方法巧妙而自然给解决了~ 贴出来共享一下。
题是这样的:证明,在任意四边形的四条边上各做一个正方形,那么连接相对的正方形中心的线段互相垂直并且等长。示意图如下。
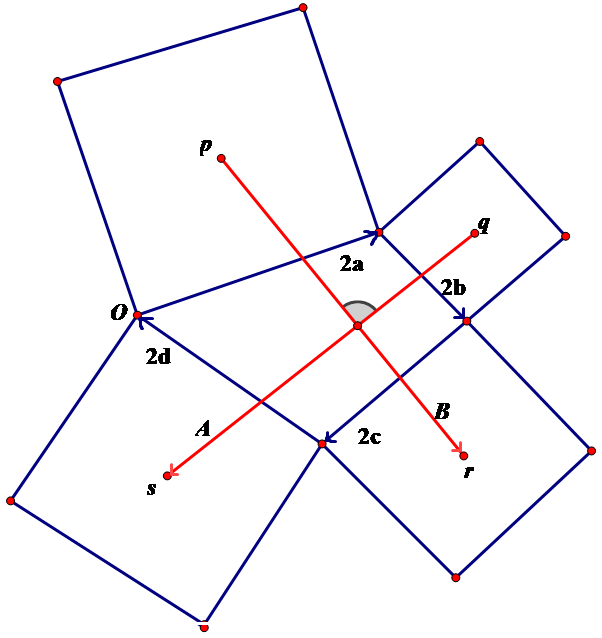
这道题的平面几何做法我已然忘却,现在的脑子也已经解不动平面几何题了。。就直接把书上的巧妙复数解法贴过来吧~
设2a、2b、2c、2d为表示四边形4边的复数(引入因子2只是为了方便),唯一的条件是这个四边形是闭合的,即a+b+c+d=0。
如果以图中O为原点,要想走到2a这条边的正方形中心,就要先走一个a,再沿着与a成直角(逆时针)的方向走过同样地距离。这样,由于ia正是a以逆时针方向旋转一个直角而得(想想复数乘法的几何意义,模相乘而辐角相加),所以p=(1+i)a。
同理,q=2a+(1+i)b,r=2a+2b+(1+i)c,s=2a+2b+2c+(1+i)d。
所以由q到s的复数A=s-q和由p到r的复数B=r-q就是 A=(b+2c+d)+i(d-b),B=(a+2b+c)+i(c-a)。
我们想要证明的是A和B垂直并且等长,而这两个命题恰好可以由一个复数命题来表达:B=iA,即A+iB=0。这里仍然是用到了复数乘法的几何意义。
而这样一来问题就归结为简单的复数运算了:A+iB=(a+b+c+d)+i(a+b+c+d)=0。
问题轻松解决!
因为我高中就没有学过数学竞赛,所以不了解用复数解平面几何题是不是属于常规解法之一,反正我看到这个解法之后还是相当震撼的。《复分析——可视化方法》这本书才刚刚开始看,就已经惊喜连连。这本书的作者坚持认为,应当用形象化的东西来帮助我们学复分析,而不是用那套我看着发晕的形式化语言,相当符合我的风味,复分析本来该是最美的数学分支,却被我们的老师搞的就成了背公式算题。并且他还宣称是继承了牛顿那套用几何方法推演微积分的方法,等我继续看下去看有没有什么更加震撼的东西再来分享吧~



连接四边形的一条对角线,取中点。将中点和4个重心连上,一对旋转的全等三角形浮现出来。为什么相似呢?只需证对边分别垂直相等。怎么证?以上面那两个为例,分别向四边形的边作垂线,垂足和中点连上,又出了一对旋转的全等。这个的证法,上过初中的都会吧。复分析很高深,正在学习中。