一个有趣的运动学问题

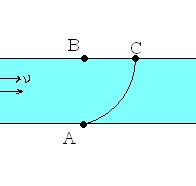Problem:一名船员从一条笔直、宽度恒定的运河一侧（A点）出发，希望划向出发点的正对岸（B点），河宽为d。河中水流的速度出处为v，而船员一直稳稳地划桨，若不计水流速度则船速也为v。他一直保持船头朝向目标（B点），但水流把它冲向下游。那么当船员到达对岸（C点）时，水流将使得船向下游漂流多远？（即BC等于多少？）从静止于河岸的观察者看来，船经历了怎样的运动轨迹？

Hint:这道题来自《200道物理学难题》，一本很有意思的书。这个问题乍看无从下手，但其解答十分巧妙简洁，并不需要太多知识。请认真思考再看提供的答案。

Solution:要注意到一点：在任何时间段内，船和目标之间距离的减少量与船被水冲下的距离相等！做一条直线l垂直于河水流动方向且使得A到l为d。这样一来，任何一个时刻船到B点的距离就等于船到l的距离，因此船的轨迹是一条以B为焦点、l为准线的抛物线！因此不难得出BC=d/2。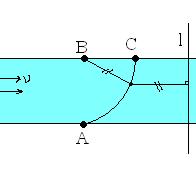

Hint2:如果你是学物理竞赛的，那么第一问还有另一种比较常规的方法，我就是用另一种方法把这道题做出来的，原题提供的这个解答估计没有几个人能想到。如果以河水作为参考系，这个问题就和那个“猎狗追兔子”的经典问题比较像了。借用那道题的办法，可以列两个式子：沿河流方向的运动学方程和船与B连线方向的运动学方程。这两个方程一联立，就可以消掉一块很难处理的东西，就把BC距离给求出来了。