最小作用量原理与物理之美2——费马原理
对于几何光学中的许许多多的定律,费马找到了一种统一的描述,现在被称为费马原理,被认为是最小作用量原理在几何光学中的特例,是最小作用量原理最早的成功例子。上一篇文章并没有真正写最小作用量原理,写的仅仅是一些简单的极值问题(千万不要认为那就是最小作用量原理),而本文与下一篇文章则将写最小作用量原理在几何光学与动力学的特例,并给出比较精确的数学公式(这是为了后面的横向比较和更深刻地理解最小作用量原理),对微积分头痛的人可以跳过公式只看文字。
费马原理是这么说的:过空间中两定点的光,实际路径总是光程最短、最长或恒定值的路径。
其中光程定义为该介质的折射率乘以路程。写成数学的形式就是:
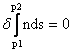
其中,δ是变分符号,p1、p2表示空间中两个固定点,n为介质的折射率,s表示路程。为了理解上式的含义,我们需要和导数做一个类比。我们对一个函数求导数,如果导数值等于零,那么可以判断出原函数在该点处会取得极小值、极大值或恒定值。上面的式子和导数有一个显著的不同,导数研究的是以字母为自变量的函数的极值,而上式想求的则是以一个函数(位置随时间变化的函数)为自变量的泛函的极值。我们把每一条路径看作是位置随时间变化的函数,把这个函数看作自变量,我们要求的则是各条路径中光程取极值的那条路径;就像我们求导求的是各个x中使得y取极值的那个点。函数求极值可以用导数,泛函求极值则可以用变分法,即δS=0(其中S是一个泛函)。大家就把δ理解成和导数相类似的东西就可以了。
大家可能还见过费马原理的另一种表述:过空间中两定点的光,实际路径总是时间最短、最长或恒定值的路径。就是把光程换成时间t了,即:
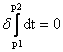
这两种表述是等价的,因为
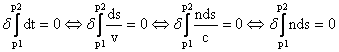
上面推导中v表示光在某介质中的传播速度(v=c/n),c表示真空中光速(是个常数),其余字母的解释和前面一样。
在几何光学中,我们把作用量S定义为
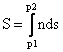
也就是说作用量在几何光学中的形式就是等号右边的那部分。
有了费马原理,就有了全部几何光学,我们可以从费马原理出发退出所有的几何光学定理。这是费马原理的强大威力之一。
首先看最简单的,光在同种均匀介质中沿直线传播,从费马原理当然一眼就能推出来。光走其他的路径肯定比直线所花的时间要长(暂不讨论广义相对论中的时空弯曲)。
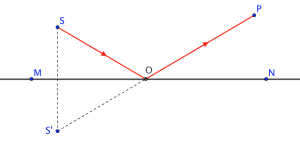
再来证明平面镜反射中反射角等于入射角。我们把S点对称到平面镜的另一边,用直线联结S’与P,得到的就是时间最短的路径,联结SO,通过简单的平面几何知识就可以得到反射角等于入射角的结论。
折射定律亦可以从费马原理推出来,但是稍显麻烦,在这里就不定量讨论了。我想说的是光之所以发生折射确实是因为光走那条关了一道弯的路径是时间最短的。记得很小的时候我就知道光可以发生折射,可是我就一直弄不明白好端端的直线光为什么不走,非要走一条怪异的拐弯的路线。我曾经问过很多老师光为什么会发生折射,他们都没有给我满意的答复,直到我看见
了费马原理才彻底弄明白了这个问题。
下面我要重点说一下费马原理如何简洁的证明圆锥曲线的光学性质。这里的圆锥曲线都被镀上了一层银,可以当镜子用。
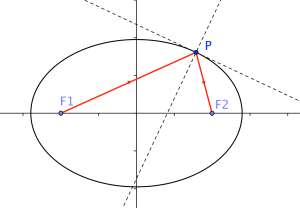
(1)从椭圆一个焦点发出的光,经过椭圆的反射,会汇集到另一个焦点上。证明:根据椭圆的定义,F1P+PF2=定值,根据费马原理,光的实际路径是光程极小、极大或定值的路径,所以F1到圆锥曲线上任意一点再到F2是光走的实际路径,所以从F1发出的光经过圆锥曲线反射会汇集到
F2。
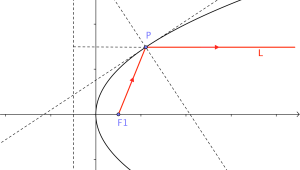
(2)从抛物线的焦点发出的光,经过抛物线反射会形成平行光束。证明:做出抛物线的准线,F1P等于P到准线的距离,即这两段光程相等。光的实际路径至于光程的取值有关,所以从F1发出的经过抛物线反射的光和直接从准线向右发出的光完全等效,因此从F1发出的光,经过抛物线反射会形成平行光束。
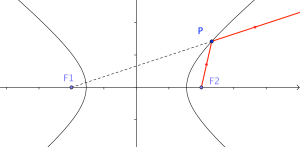
(3)从双曲线的一个焦点发出的经过双曲线反射形成的光,好像是从双曲线的另一个焦点直接发出的。证明:因为F1P-F2P=定值,所以对极值的取得没有影响,即从F2发出的经过P反射的光与从F1直接发出的经过P的光取极值的路径相同,即路径是一样的。故证明了双曲线的光学性质。
要知道,从数学上证明上述性质是相当麻烦的,而有了费马原理则可以几句话就把问题解决,一点高深的
数学也没用。这是费马原理的另一个强大威力。
至于费马原理为什么是对的,《费恩曼物理学讲义 第二卷》第19章给出了一个精彩阐述。他是这么说的:“要是他遵循一条需要不同时间的路径,则当它到达时就有不同相位。而在某一点上的总振幅等于光能到达的所有不同路径振幅贡献的总和。所有那些提供相位差异很大的路径将不会合成任何东西。但如果你能找出一整序列路径,他们都具有几乎相同的相位,则小小的贡献便将加在一起而在到达之处得到一个可观测的总振幅。因此,重要路径就成为许多能给出相同相位彼此靠近的路径。”而只有时间取极值的那条路径,才能保证路径有微小变化时时间保持不变(再次与导数类比,函数取极值的那个点,当x有微小变化Δx时,Δy=Δx*y’=0,其余的点Δy都是一个不为0的数)。因此,时间取极值的路径被叠加了,成为了实际路径,而其余的任何可能路径都被不同的相位给抵消没了。
这个甚至可以解释光的衍射现象。当我们用一个很细的狭缝来挡住一部分光时,时间不取极值的某些路径也因为有一部分光被挡住而不能很好的叠加为零,因此这种情况下光并不是总衍直线传播,而是产生了光可以绕到障碍物后面的的现象,即衍射现象。
我们已经看到了最小作用量原理在光学中的应用,它可以代替所有其他几何光学定律。下篇文章我将写最小作用量原理在力学中的特例,以及如何代替整个牛顿力学。



不知道大家以前对费马原理了解的有多少…
费马定律有点非因果、形而上的,作为本质来看不妥。我觉得本质是光传播的测地性质,就好像变分法求解和微分方程一步步推的关系一样。
帅~
说的很浅显易懂!谢谢!!