代数基本定理的一个最简单证明

//看懂本文需要且仅需要关于复数的基本概念。

代数基本定理，是指任何一个一元复系数多项式都至少有一个复数根。从代数基本定理可以很显然的推论出我们可能在初中就已经熟悉的一个结论：一元n次方程必有n个根。虽然大家都已经对这个定理感到习以为常，但是其实它并不是显然的，因为如果只考虑实数，一元n次方程就不一定有根。当把研究对象拓展到复数时，一下子所有代数方程就有解了，这其实是一件很不显然的美妙结论。

关于代数基本定理，有很多很多种证明方法。貌似第一个证明是牛逼哄哄的高斯在博士论文中给出的…基本所有的证明方法都或多或少的用到了一些比较高等的数学，对于只有高中数学知识的人来说很难看懂。即使是《什么是数学》里给出的证明，也用到了一个并不是那么好理解的“卷绕数”的概念。但是，下面要给出的证明，只需要有关于复数的基本概念就可以理解，只要几句话就证明完毕了！此证明由北大数院的范后宏老师在“古今数学思想”课上提供。

代数基本定理证明：

设$$w(z)=z^n+a_{n-1}z^{n-1}+…+a_0$$

于是我们想要证明的结论就是：一定能找到某个z，使得w(z)=0。

我们先把z写成$$z=re^{i\theta}$$的形式。

首先，我们考虑r=0的情况。这时w(0)将是复平面上的一个点，并且这个点就是a0，且a0不等于0。（如果a0等于0那z=0就是原方程的解了，定理直接得证。）

然后，我们再考虑0<r<∞的情况。对于一个固定的r，如果这时我们让θ从0到2π连续变化，那么对应着w(z)将会在复平面上画出一条封闭的曲线，如下图。这个曲线可能是很扭曲的形状，也不一定是绕了一圈的，可能绕了很多圈。比如w(z)=z^2，当z的辐角从0到2π连续变化时，w(z)将在复平面上绕着一个圆转两圈。在这里我们并不关心这条曲线的具体形状。

最后，我们再考虑r->∞的情况。此时当z的辐角从2π连续变化时，显然w(∞)的所有值都将是无穷大（因为此时只有z的最高阶项是起作用的，而它前面的系数是1），对应着就是w(∞)将在复平面上的无穷远处画出一条封闭曲线，见下图。

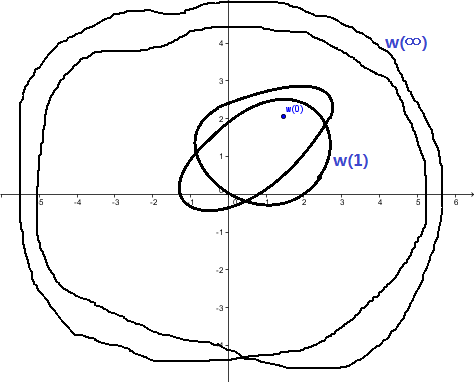
于是，当r连续的从0变化到∞时，这条曲线将从一个点连续的变化成一条跑到无穷远处的闭合曲线。于是，其中必有某一条曲线经过了0点，于是命题得证。

证毕。

用更加形象化的语言，此证明只有一句话：在未名湖中的一点扔下一颗石子，将激起一圈不断扩大的涟漪，在涟漪到达湖边之前，它一定会经过指定的一个点。

当然，如果要追求严格性的话，这种“证明”并不算是严格证明的。但是它却将一个并不是很显然的命题变得非常形象化，某种意义上来说可以显然的看出它是对的，我觉得对于一个学物理的孩子来说这就已经足够了。