点猜想
作者： physixfan
首先在平面上任意给定不全共线N个点，然后在点之间连线，以保证任意两个点之间都有直线连接。所谓点猜想就是说，在这样的情况下，总存在直线仅过两个点。
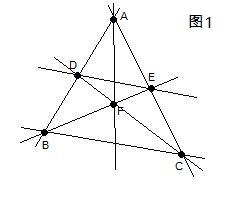如果给定了A~F六个点的位置如图，则整个图形形状就是左图，DE和AF就仅过两个点。你可以简单尝试一下，试着自己画几个点，你会发现确实无论如何也不能让所有的直线都通过三个或三个以上的点。
这个问题是小时候就见过的，在苦苦思索了好一阵子无果之后就给渐渐淡忘了。今天去图书馆看书偶然间又看到这个问题了，觉得还是挺有意思的，不过还是没什么思路。上面的介绍居然说，点猜想在被提出之后几十年内没有人能够证明！看似如此简单的问题居然还难倒了一大批人呢！但是，当最终证明被发现时，虽然思路非常灵活巧妙，却是异乎寻常的简单，连初中生都能看懂！不知你能不能自己证出这个猜想呢？
证明如下：
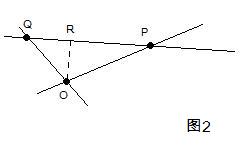
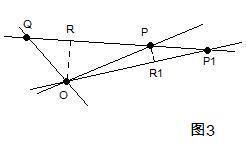
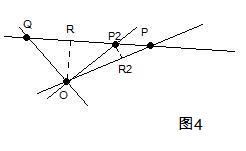
作出所有点到所有直线的距离，取出这些距离中最小的那一个，当然那些在直线上的点到该直线距离为零不算在内。假设如图2所示的点O到直线PQ的距离OR就是那个最小的距离。下面我将断言：直线PQ上不可能存在第三个点。因为：如果存在第三个点并且在线段PQ外侧（如图3），则距离PR1将小于OR，与假设矛盾；如果存在第三个点并且在线段PQ之内（如图4），则距离P2R2将小于OR，也与假设矛盾。因此直线PQ上只有两个点PQ。证毕。
这个证明思路很好啊，假设最小然后找到更小来反证。据学数学竞赛的人说这是一个常见的证明方法，真后悔当时没去听听数学竞赛课…
9 Comments
Post a comment
这个问题折腾了西尔维斯特先生一辈子，结果被这么简单的方法搞定了。估计他在天堂看到这个证明要哭的。
还有人真的很投入的研究这种小问题吗
我觉得就像一个人所说的（虽然说的不是这个问题） 这个问题迟迟不被解决仅仅是因为没有一流的数学家去研究它…
看下面链接：
http://www.math123.cn/sxsh/574.htm
这个问题迟迟不被解决仅仅是因为没有一流的数学家去研究它。。。。这句话出处在这里：
一次拓扑课，Minkowski（闵可夫斯基）向学生们自负的宣称：“这个定理（指四色定理）没有证明的最要的原因是至今只有一些三流的数学家在这上面花过时间。下面我就来证明它……”于是Minkowski开始拿起粉笔。这节课结束的时候，没有证完，到下一次课的时候，Minkowski继续证明，一直几个星期过去了……一个阴霾的早上，Minkowski跨入教室，那时候，恰好一道闪电划过长空，雷声震耳，Minkowski很严肃的说：“上天被我的骄傲激怒了，我的证明是不完全的……”
摘自《Heroes in My Heart》
哦对 就是这里 刚刚看的Heroes In My Heart…
那句签名档确实经典：
美丽有两种
一是深刻又动人的方程
一是你泛着倦意淡淡的笑容
《Proofs from THE BOOK》 里有这个问题的多种变形和证明。
P.S. 这个问题不能算小问题，它本身的作用可大了。
那本书我买了 不过是英文的 估计一时半会儿是看不懂了
还有很大作用？看来是我小看它了…
数学史上经典的一题～能激励所有的民科激流勇进的绝佳材料～
呵呵 是啊 不过一般民科都没什么文化 估计不会知道这个题吧