生物界的标度率
如果把我们的身体所有部分按照比例放大或者缩小10倍,我们是否可以仍然活的很正常?为什么蚂蚁之类体型很小的生物在相对于他们身高好多好多倍的地方摔下来也不会被摔死,而我们人类就不行?跳蚤真的是传说中生物界的跳高冠军?只要经过简单的物理分析,一切答案便变得显然。
不靠谱的大人国

没学过物理的人,常常以为世界是可以按照比例任意的放大缩小而不会引起什么严重后果的。比如说一本非常有名的小说《格列佛游记》中就出现了大人国和小人国这样的设定,里面的大人和小人只是把正常人类按照比例把身体各部分放大缩小了。虽说这只是本小说而且甚至算不上科幻小说,但是这也不妨碍我们以死理性派的角度去看看它到底是不是存在着物理上的bug。
我们先看看大人国的境遇。我们必须假设,当体型放大之后,构成身体的基本构造都是一样的,即都是同样的元素、同样的分子同样的蛋白质在起作用,因此,大人国的人们的身体密度一定是与普通人类一样的。于是,他们的体重m=ρV∝l^3,其中l为身高。然而,我们再看看单位面积上骨头要承受的力:F/S=mg/S∝(l^3)/(l^2)=l。这是个什么概念呢?意思就是,你体型越大,你单位面积上骨头要承受的力越大,也就是说大人国里的人要比我们容易骨折的多。
在生物界里这一现象可以很明显的得到反映。不知道大家有没有注意到,如果你把一张蚂蚁的照片和一张大象的照片放到大小一样去比较,会很明显的发现大象的腿要粗得多。如果把蚂蚁按照比例放大到大象那么大,按照上一段中的分析,它是一定站不起来的。因此大象为了能站立,它就必须让自己的腿变粗好多。
其实标度变换下物理现象不是不变的这一事实早就被人们所认识了,物理界的开山鼻祖伽利略就在其著名的《关于两种新科学的对话》中提到了这一事实,下图就出自该书。即如果一个动物的体型长度被放大了两倍,那么其骨头的粗细程度必须和原来不成比例。
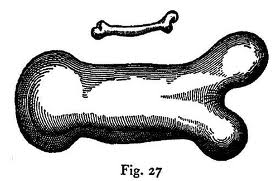
小人国的境遇
那么小人国里的生活又是怎样的呢?按照上一部分的分析,他们骨折的可能性就会小得多,但是他们也有他们自己的困扰。比如说视力。按照光学的理论,眼睛最小分辨角的极限θ=λ/D,D为瞳孔直径。因此θ∝l^-1。这将导致比较悲剧的后果:假定他们的身形比我们小10倍,明视距离也比我们小10倍,那么,鉴于他们的最小分辨角比我们大10倍,他们的书上印的字应当和我们的一样大,然而书中每行的字数必须比我们小10倍,每页里的行数也要少10倍。
在动物界中也确实存在着类似的问题,因此为了视力不至于太差,体型比较小的动物的眼睛在身体中占得比例都偏大。婴儿一生下来的时候体型比我们小很多倍,可是眼睛的大小却基本已经和成人一样了。像老鼠之类的小动物也是,他们的体型基本有人类的1/10吧,可是眼睛大小却明显比1/10要大。而为了保持一样的视力,具体眼睛大小与身型是几次方的关系,这就需要详细讨论了,此文不再详述。
蚂蚁为什么摔不死

生活经验告诉我们,我们似乎从来没有见到过蚂蚁摔到地上摔死,尽管跌落的高度已经是它身长的好多好多倍了。而我们人类只要从比身高高几倍的地方摔下来就基本一命呜呼。这是为什么呢?
前面提到的体型越小越不容易骨折是一方面原因,可是蚂蚁的腿相对于大型动物来说已经很细了,除此之外其实还有另一个原因。我们考虑空气阻力。当从很高的高处跌落时,由于空气阻力的作用(在速度很小时,空气阻力正比于面积且正比于速度),最终下落速度将是匀速的,称之为极限速度v,此时空气阻力和重力平衡。mg∝l^3,而空气阻力f∝S∝l^2,因此v∝l。对于蚂蚁来说,体型如此之小,以至于极限速度就会变得很小,不论从多高的地方落下,它只要能承受这么大的落地速度就足以摔不死了。
动物跳高冠军是跳蚤?
有一个流传很广的说法,说跳蚤是自然界中的跳高冠军,它以那么小的体型就能跳出1米的高度,如果他长得像人那么高,就能跳出1千米的高度了!这个不靠谱的说法仍然是犯了直接按照几何比例去放大的错误。
为了研究不同生物跳到的高度,最靠谱的一个假设是假设对所有的动物,每单位质量上的肌肉所提供的能量大体相等。如果按照这个假设,那么跳到高度h所需要的能量为mgh∝m∝l^3,而肌肉所能提供的能量E∝m∝l^3,因此h应当与l无关!于是乎,理论上来说,不论多大的动物,他们能跳出的最高高度都应当是大体相等的!(当然,有些动物就没有进化出特别适合跳跃的肌肉,他们当然跳的不高。)于是,要比较各种生物到底谁是跳高冠军,只要直接比较高度就好了,倘若除以身高,那就自然是谁矮谁沾光了~
本文的这些分析,都属于物理中称为量纲分析的方法。虽然得出的结论并不精确,但是至少它在定性上是正确的。在定量研究问题之前,先通过简单的分析得到定性的结论,往往是十分重要的。
主要参考书:《定性与半定量物理学》赵凯华著。 //原载于果壳网

