复数方法巧解平面几何题
快放假了才买到《复分析——可视化方法》这本书,相见恨晚啊,这本神书,如果我能早点读,这学期的复变函数估计就学的不会这么吃力了。。。在这本书开头的地方有一个用复数方法解决平面几何问题的例子,我一看便惊了:这正是我初中时候见到的一道印象极其深刻的平面几何题,曾为它绞尽脑汁也没有想出做法呢,然而这本书就用复数的方法巧妙而自然给解决了~ 贴出来共享一下。
题是这样的:证明,在任意四边形的四条边上各做一个正方形,那么连接相对的正方形中心的线段互相垂直并且等长。示意图如下。
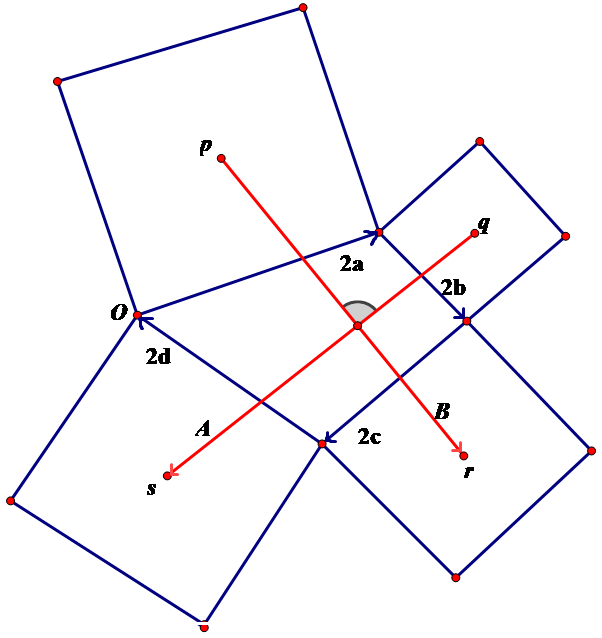 …
…
椅子的稳定性问题
4条腿长度相等的椅子放在起伏不平的地面上,问是否一定可以找到一个位置使得四条腿同时着地而放稳?
这个问题我在初中的时候就听赵一夫跟我说起过,当时觉得这问题太诡异了,怎么下手啊。今天再一次见到仍然觉得无从下手,看了答案之后顿觉奇妙。答案是肯定的,一定可以找到一个位置使得椅子放稳!
题目的条件先解释一下,4条腿长度相等实际上告诉了我们这4条腿的顶点是共面的。看了网友的回复,确实题目里有隐含条件需要明确地写出来:(1)椅子是正方形的…(2)四条腿的长度相对于地面的起伏来说足够长…(3)只要四条腿同时着地就称之为放稳(即认为地面的摩擦系数无穷大)…(4)起伏不平的地面我们要把它理解成是一个连续的二元函数。…
几个数学娱乐
今天六一,这个曾经属于我们的节日。岁月无情的在我日渐苍老的脸上刻上了印记,看到照片上小时候稚嫩的我,看到肯德基里面孩子们无忧无虑欢乐的笑脸,我总有种莫名的感伤。今天写下几句小的数学娱乐,来祭奠逝去的似水年华。虽然我们不能企图永远年轻,但至少可以像小孩子那样笑颜永驻。
1.我已经证明了著名的数学难题:任何一个偶素数总能写成两个奇数之和。
2.对于这个数学难题:方程n^a+n^b=n^c对于n>2没有正整数解,我已经找到了一个极其简单的证明,甚至一页之内就能搞定。
3.我已经想到了一个绝妙的宇宙万能公式,只不过这里空白太小,写不下…(这句话曾经是我的校内网状态和QQ个性签名,用在有字数限制的地方特别合适)
4.原来任何进制都是10进制..
5.世界上有10种人,一种是懂二进制并且看贴回贴的人,一种是不懂二进制或者看贴不回帖的人……
3.14 Today Is Pi Day!
又是好久没有写什么东西了 哎 越是在家闲着就越懒 今天是传说中的白色情人节 不过这跟我没什么关系 今天还是Pi Day 那就说说Pi吧 顺便再熟练一下Tex
首先写一些有关$$\pi$$的漂亮的表达式。第一个表达式是最常见的一个,也就是这个表达式曾经激起了我无尽的好奇心,引我走上了自学微积分的道路。其证明在这篇文章中有。
$$\frac{\pi}{4}=1-\frac{1}{3}+\frac{1}{5}-\frac{1}{7}+\frac{1}{9}-\frac{1}{11}+…$$
$$\frac{\pi^2}{6}=\frac{1}{1^2} + \frac{1}{2^2} + \frac{1}{3^2} + \frac{1}{4^2} + \cdots $$…


