e,一个常数的传奇
自然对数的底e是一个令人不可思议的常数,一个由lim (1+1/n) n 定义出的常数,居然在数学和物理中频频出现,简直可以说是无处不在。这实在是让我们不得不敬畏这神奇的数学世界。
欧拉恒等式
但凡说起e,一个必定要提到的公式就是欧拉恒等式——被誉为世界上最美丽的公式。
$$e^{\pi i}+1=0$$
数学中最基本的5个常数——0、1、圆周率π、自然对数的底e和虚数单位i,以及数学中最基本的两个符号,等号和加号,就这样通过一个简单的恒等式联系在了一起,实在是让人叹服。
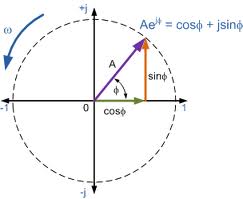
这个等式有个一几何的直观解释。一个实数在实数轴上可以用一个向量表示,旋转这个向量,就相当于乘以一个虚数i。据此建立一个以实数为横轴,虚数为纵轴的坐标系。实单位向量,每次逆时针旋转π/2, 可以分别得到结果1,i,-1,-i,1. 即转4次以后就回到了原位。而当实单位向量保持长度不变旋转θ角度,得到的向量就是:cosθ+isinθ。根据欧拉公式 e iθ = cosθ+isinθ可以看出 e iθ 就代表实单位向量1旋转θ角后而得到的向量。所以 e iπ 意味着单位向量逆时针旋转了π,结果显然是-1。
增长规律
这个世界上有许许多多的事物满足这样的变化规律:增长率正比于变量自身的大小。例如放射性元素衰变的时候,衰变率就和现存的放射性物质多少成正比;资源无穷多的社会,人口出生率将(近似的)和现存人口数成正比等等。而此类变化规律所确定的解,则是由以e为底的指数增长所描述的:如果x的变化率等于变量x自身的λ倍,那么该变量随时间t的函数则为
$$x=Ce^{\lambda t}$$(C是任意常数)
而e的直观含义正是增长的极限,这个问题在 数学常数e的含义 中有过详细的介绍。
正态分布
…神秘的本福特定律
统计一下世界上237个国家的人口数量,你觉得其中以1开头的数会占多大比例,而以9开头的数又占多大比例呢?如果你的回答是都为1/9,恭喜你你是正常人,但是事实却不是如此:以1开头的数惊人的占到了27%,而以9开头的数却只占5%。下图可以很形象的展示出在各国人口数量问题上,以各个数字开头的数占了多大的比例(图片来自维基百科)。为什么会相差这么大呢?这正是神秘的本福特定律在起作用。
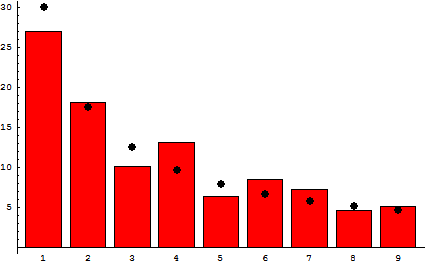
本福特定律,也称为本福德法则,说明一堆从实际生活得出的数据中,以1为首位数字的数的出现机率约为总数的三成,接近期望值1/9的3倍,推广来说,越大的数字,以它为首几位的数出现的机率就越低;精确地数学表述为:在b进位制中,以数n起头的数出现的机率为logb(n + 1) − logb(n)。
在十进制中,首位数字出现的概率为:
| d | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
| p | 30.1% | 17.6% | 12.5% | 9.7% | 7.9% | 6.7% | 5.8% | 5.1% | 4.6% |
量子永生
MWI(Many World Interpretation)平行宇宙理论(或多宇宙理论)是一个非常有意思的理论,它的提出是为了解释哥本哈根学派所面临的困难。
在解释著名的薛定谔的猫时,哥本哈根学派认为在观测前,猫处于既死又活的状态,然而一旦观测,波函数就坍缩了,我们有50%的概率观察到它死了,50%的概率观测到它还活着,但是现实世界里猫只有死或者活之中的一种状态。但是这种解释有一个问题,就是观测到底是什么意思,观测者是什么,用仪器记录下来而我们人类不去看,波函数到底坍缩了没有,最终会把问题归结到意识上面,一个拥有意识的“观测者”成了宇宙中拥有使波函数探索的至高无上的权利,似乎与我们对世界的认识不符。。
于是,平行宇宙理论粉墨登场~!MWI解释说,每次实验都会同时产生一只活猫和一只死猫,只不过他们存在于两个平行宇宙中,一个宇宙中猫死了,而另一个宇宙中猫还活蹦乱跳!当一个量子过程发生后,不光是猫被卷入了叠加态,整个宇宙也被卷入了叠加态!不同的平行宇宙之间不能产生任何联系,而我们也只能按照一定概率观测到某一个平行宇宙,这就解释了薛定谔的猫实验。时至今日,平行宇宙理论的支持者势力已经仅次于哥本哈根解释了,它在物理学界已经可以算是一种被广泛接受的正规理论了。
如果我们接受平行宇宙理论,那么就会得到很多有意思的结果。
你在这个世界为你错误的选择而痛苦,而这正是身处另一个量子分支的你快乐的表现。而这并不是最让人欣慰的结果,根据平行宇宙理论,你甚至是永生的~!…
潜水艇悖论
在爱因斯坦的狭义相对论提出之后,人们就从它出发提出了各式各样奇妙的悖论,比如著名的孪生子悖论、堵火车悖论等,仔细分析这些悖论到底是怎么被消除的,将十分有利于加强我们对相对论的理解。目前我见过的最难想的悖论,莫过于这个“潜水艇悖论”了。
首先假设一艘完全浸没在海中的潜水艇,在相对海水静止时能不升不降地正好保持平衡,然后再假设它在与海面平行的方向上以接近光速行进。基于物体长度会在运动方向上收缩的相对论效应,在海面上固定船只上相对海水静止的观察者看来,潜水艇本身会收缩,密度会变大,并最终下沉。但潜水艇上的船员们看到的却是飞速向后的海水在收缩,密度在变大,他们会得出结论认为,由于海水密度变大后产生更大浮力,潜艇将漂浮而上。按照相对论,两种看法似乎都没有错,潜艇到底是沉或浮的悖论由此而生。…
有趣的无规行走模型
昨天和一帮子同学出去玩,晚饭时间点完菜等待上菜的时候有两个同学玩起了一个非常无聊的游戏:甲同学扔硬币,乙同学猜正反面,如果乙猜对了则乙的鼻子变长1cm,反之如果乙猜错了则鼻子缩短1cm。(这个是和谐过的版本,原始版本变长变短的不是鼻子而是另一个猥琐的东西…)。他们正在无聊的玩,全然不知道这么玩下去他鼻子长度的绝对值期望是多少…其实,这正是我高一的时候在费恩曼物理学讲义上看到的一个数学模型:Random Walk(无规行走)。对于这个模型,我敢说绝大多数人凭直觉会觉得鼻子长度的绝对值最终的期望值会是0,但事实绝非如此,你可以自己扔几次硬币试试,正确的答案应该是你扔硬币次数N的平方根!
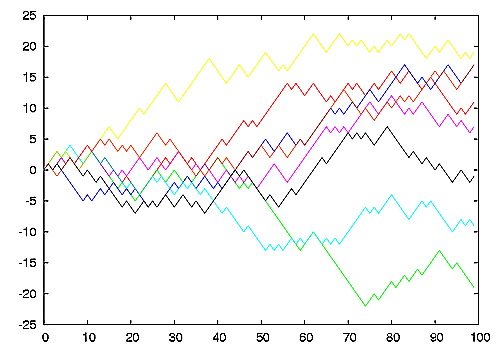
下面给出证明,该证明基本来自《费恩曼物理学讲义》第一卷:…
《哥德尔 埃舍尔 巴赫——集异璧之大成》
最近正在家拜读传说中的旷世奇书《哥德尔 埃舍尔 巴赫——集异璧之大成》。当我刚刚看完第一章的时候就已经完全被这本书给镇住了,而且越往下读越被这本书深深的震撼。读这本空前的奇书带给我的精神上的愉悦感甚至要大于跟美女聊天…
哥德尔Godel是伟大的数学家(参见这篇文章),埃舍尔Escher是诡异的画家(参见这篇文章),巴赫Bach是人尽皆知的音乐家。《集异璧之大成》这本书讲了这三个人,三个完全不同的领域,结果你会发现这三个领域不仅仅是具有深刻联系,而且甚至可以说他们是一个统一体的三个不同侧面!英文版的封面画(下图)很好的反映了这一点。
 …
…


