湍流 Spectrum 与 Cascade 的理解
//本文是我在知乎上的回答《学物理过程中,你有哪些问题是当时理解的比较肤浅,后来突然豁然开朗了?》。
近期在研究湍流有关的东西,就说说对湍流 spectrum 和 cascade 的理解吧。
最初接触湍流的 spectrum 和 cascade 是著名的 K41 Theory (Kolmogorov 1941 Theory) 。针对三维流体,通过假设湍流在小尺度上各向同性,再假设存在一个不是k的函数的常数 energy dissipation rate \(\varepsilon\)(意为单位时间内耗散掉的能量),那么我们可以一定的空间尺度范围内得到三维流体的 energy spectrum:
\[E_k=C\varepsilon^{2/3}k^{-5/3}\]其中k是波数;\(E_k\) 是 energy spectrum,它是能量的傅里叶变换,它与能量的量纲关系为 \([E]=[E_k]*[k]\)(需要注意的是,流体里说的所谓能量其实是通常含义下的能量密度除以质量密度,即 \(E\sim\mathbf{v}^2\),v为速度);C是一个 universal 的无量纲常数。Energy spectrum 的图像如下图(双对数坐标):
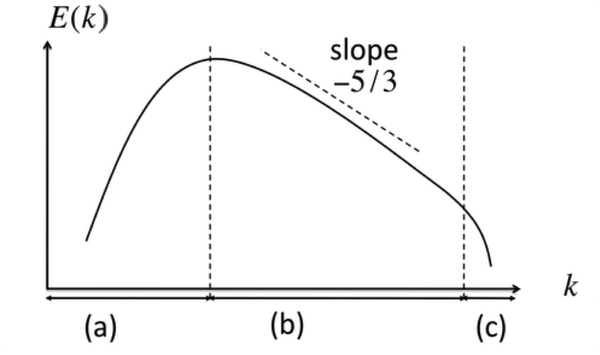
斜率 -5/3 是 K41 理论的著名结论,已经被无数数值模拟所验证。得到这个 -5/3 的方法其实异常简单:因为假设了一个不是k的函数的常数 energy dissipation rate \(\varepsilon\),那么对体系所涉及到的物理量直接进行量纲分析就能得到它。
湍流的能量会形成一个 energy cascade。如果能量从大尺度(小k)注入,比如拿着棍子搅一缸水,那么能量会沿着那个 -5/3 的直线从大尺度(小k)往小尺度(大k)流动,大漩涡破碎成小漩涡,小漩涡破碎成更小的漩涡,最后动能在一个很小的尺度上被耗散掉,动能转换为内能,卡通图如下:
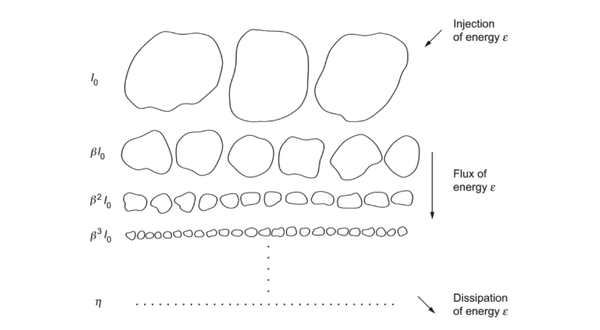
著名的斜率 -5/3 可以直接通过量纲分析得到,而且能量尺度越来越小的 cascade 非常直观也非常自然,当时我学到这里就觉得挺满意的觉得已经理解了这些现象了。而且通常的流体力学、湍流教材对这个话题也就只介绍这些内容了。
—————————————————————————————————-
直到后来见到了二维流体湍流的相关内容,颠覆了我的认知。出乎我意料的是,二维流体的湍流 spectrum 和 cascade 性质和三维流体非常非常不同。
二维流体的 energy spectrum 图像是下图的样子:
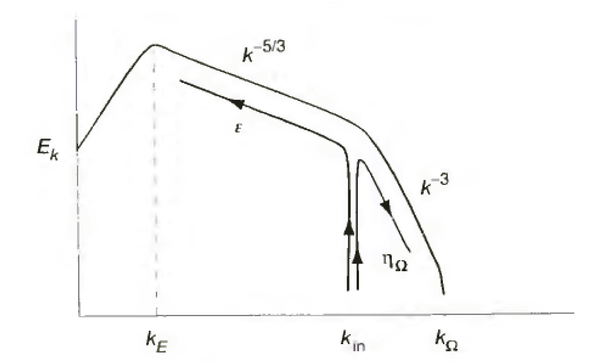
除了著名的 -5/3 斜率之外,还有另外一段斜率 -3 的直线!斜率 -5/3 是由常数 energy dissipation rate \(\varepsilon\) 所决定的,而斜率 -3 则是由常数 enstrophy dissipation rate \(\eta_\Omega\) 所决定的。其中 enstrophy 的定义为 \(\Omega=\int|\nabla\times\mathbf{v}|^2 d\mathbf{x}\) ,v是速度。
而且由上图所示,二维流体的 cascade 也变得完全不同了。在二维流体里,energy cascade 的方向是能量由小尺度(大k)往大尺度(小k)流动的!!!这被称为 inverse cascade。而 enstrophy cascade 则由大尺度(小k)往小尺度(大k)流动,与三维流体的 energy cascade 方向一致,这被称为 direct cascade…
虽然我知道假设了常数 enstrophy dissipation rate 的确可以同样的通过量纲分析得到另外一个斜率 -3,可是为什么在二维流体的 energy spectrum 上就有两段斜率不同的直线,三维流体里就只有一段呢?为什么二维流体湍流里能量会往大尺度走,最后在最大的尺度——系统尺度上耗散掉呢?!
在看到了MHD湍流(MagnetoHydroDynamics Turbulence,磁流体湍流,即等离子体做流体近似后得到的系统,与普通流体的主要区别在于洛伦兹力的出现)的 spectrum 和 cascade 之后,我见到了更加丰富的现象。energy spectrum 上的斜率又有了新的数字,cascade 也是既有 inverse 也有 direct 的。这里就不详细写了。
现在对于各种维数各种流体的 spectum 和 cascade 的理解是这样的:
系统里的 ideal invariant 是决定 spectrum 和 cascade 最重要的因素。所谓的 ideal invariant,是指系统在耗散为0且外加源为0时的守恒量。当系统耗散不为0时,要想维持系统在时间上稳定,也就需要外加源,源和耗散构成了 cascade 的要素。Cascade 的方向是可以通过 ideal invariant 来计算的,其过程较为复杂,但是基本思想是这样的:首先研究系统耗散为0的情况,通过平衡态统计力学算出来所有 ideal invariant 随 k 的关系(与有耗散时完全不同),如果是peak在 k 大的地方,则说明该 cascade 是朝向 k 大的方向,最后再假定耗散不会改变 cascade 的方向就可以得到真实 cascade 的方向了。
比如二维流体,它满足的是二维 Navier-Stokes Equation,能量在耗散为时且外加源为0就是一个守恒量。但是要注意的是能量不是唯一一个守恒量,此系统还有第二个守恒量:enstrophy,这也就是为什么在二维流体的 energy spectrum 里会有第二段斜率不同的直线。能量并不比 enstrophy 更特殊,enstrophy 也和能量一样有耗散,外界向系统可以输入能量也可以输入 enstrophy。通过前述的计算 cascade 的方法,可以算出来 energy cascade 的方向确实是朝着大尺度(小k)方向的… 虽然直观上这一点仍然难以理解,不过现在起码在数学上懂了原因。
比如三维流体,它满足的是三维 Navier-Stokes Equation,能量仍然是个 ideal invariant,但是 enstrophy 就不是了。不过需要指出的时,其实能量在三维流体里也不是唯一的守恒量,还有一个守恒量是 hydrodynamical helicity \(H^K=\int\mathbf{v}\cdot(\nabla\times\mathbf{v})d\mathbf{x}\)。计算一下 hydrodynamical helicity cascade 的方向,可以发现与 energy cascade 一致,都是大尺度(小k)到小尺度(大k)。这就导致了一个微妙的结果:因为两个 cascade 方向一致,我们又无法只注入 hydrodynamical helicity 而不注入能量,因此无法得到一个单独的 hydrodynamical helicity cascade;而二者联合时, 表现行为仍然是斜率 -5/3。这也就是为什么平常我们谈论三维流体的时候很少见到有人提到 hydrodynamical helicity cascade 的原因吧,毕竟考不考虑结果都是一样的。。。
MHD 里的情况就不详谈了,直接截图一张表以作总结吧:

//主要参考资料:D. Biskamp, Magnetohydrodynamic Turbulence (Cambridge University Press, 2003).



feadcasfv