由哥白尼原理推导人类文明灭亡时间
/*这篇文章的主要内容由热学欧阳颀老师所讲 出自某期New York Times*/
下面要进行的一段推导,将十分诡异,可能有点莫名其妙的感觉,不过还是请完整看下去~
首先说一下什么是哥白尼原理。
Copernican principle:
The best theories are those that do not require the observer to live in a special place in the universe or at a special time in history in order to be true.
也就是说,一个好的理论必须满足,我们既不在宇宙中的一个特殊位置,也不处在一个特殊的时间。这个原理我想大家都可以承认吧。
为了热身,我们先推导一下柏林墙倒塌的时间。
柏林墙于1961年建立,而原文章作者Dr. Gott偶然地于1969年去了一趟柏林墙,此时柏林墙已经存在了8年。
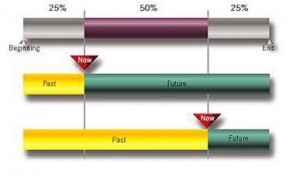
上图中,第一行整体表示柏林墙从建立到最终倒塌的整个生命历程。其中中间50%被染成紫色,这个50%是作者自己设定的,他将给出一个时间区间,而柏林墙倒塌的时间在这个区间里面的概率为50%。
根据哥白尼原理,作者访问柏林墙的这个事件是完全随机的,它落在上图第一条线段上任何一个点的概率是均匀分布的,因此这个点落在紫色区域的概率是50%,也就是说,他去访问柏林墙的时间点处在柏林墙整个生命历程的25%~75%之间的概率是50%。
若他访问的时刻位于第二条直线上的Now位置,也就是说,处于柏林墙生命历程的25%处,那么由此推算,柏林墙的寿命将还有24年(8年占25%,则剩下75%代表24年)。
若他访问的时刻位于第三条直线上的Now位置,也就是说,处于柏林墙生命历程的75%处,那么可以算出,柏林墙的剩余寿命将只有8/3年(8年占了75%,剩下的25%只有8/3年)。
因此,他访问的时刻位于紫色区域时,推算出的柏林墙剩余寿命是在8/3年~24年之间的,因此他声称,柏林墙在未来8/3~24年内倒塌的概率是50%。
当然他也可以把一开始的概率设置成60%或者其他数字,这样将推算出来另一个时间区间,柏林墙生命历程终止于这个新时间区间的概率将为60%。
最终,柏林墙于1989年倒塌。其实,作者写这篇文章的时候已经是90年代了…
下面,他又用同样的方法,给出了人类文明灭亡时间的推算。

这篇文章说人类文明已经存在了200,000年。暂且不管这个数是怎么来的,是从什么人种开始出现算起的,反正差不多。
还是设第一行为整个人类文明进程,其中中间95%被染成紫色。
那么,根据哥白尼原理,我出生这个事件,在整个人类文明进程上应该是均匀分布的,也就是说我出生时间落在紫色区域的概率是95%。
若我出生在第二行的Now位置,人类文明将持续7.8百万年;而若我出生在第三行的Now位置,则人类文明只剩下5100年。
因此得出结论,人类文明在5,100~7,800,000年内灭亡的概率是95%。
整个推导过程没有用到任何现实的数据,居然就能够把人类文明灭亡时间推算出来,非常诡异神奇…而且跟2012世界末日论貌似比较冲突…因此我们不必太担心人类会在近几年内灭亡哈~~
有人可能在想,如果我一个原始人,我存在的那个时刻人类文明只进行了100,000年,用同样的算法进行计算,算出来的人类文明灭亡时间岂不是不一样了?这个算法不就错了吗?…其实,这并不能说明这个算法错了,本来这个灭亡时间就应该随着人类文明已经存在的时间而变化。作为类比,假设全中国所有人的平均寿命是75岁,作为一个已经成功存活了20年的你,寿命期望是多少呢?75岁还是比75岁多?答案应该是多于75岁,因为所有人口的平均寿命包括了一些0岁1岁就死亡了的人,而这样的可能性对你已经不存在了,要了解你的预期寿命应该统计所有活到过20岁的人的死亡年龄作平均,而这肯定大于75岁。如果这个还是不理解,可以想象一个已经活了80岁的人,他还能活的年数期望应该是多少?你肯定不会说是-5岁吧…预期寿命的确随着年龄的增加而增加,同样的,人类文明灭亡时间也应该随着人类文明已经存在的时间而变化。
至今我仍然觉得这个推导方法特别诡异,却相当有道理,说不出它哪里不对…就当个冷笑话看看行了…



很有趣
柏林墙 选的很特殊 ,选的人也认为他很特殊啊
我觉得问题在于他有一个假设那就是人类或者柏林墙倒塌或者whatever在任意未来时间倒塌的可能性是相等的。
比如,人类在2011年毁灭的可能性跟人类在3011年毁灭的可能性相等。。
其实应该不是相等的吧。。
区别在于,柏林墙那个例子中,你的计算要基于“1989年倒塌”这个信息,也就是说,上面的所谓在一段时间内平均分布是在“整个过程结束于1989年”这个前提之下的分布和预期。这样的条件分布和条件期望就和原问题不一样了。
人出生时间不是随机的。不同时候人口不同。
的确是很有意思的推导。
但是正如倒数第二段所述,对人类灭亡时间的推导还是用了现实的数据了,那就是人类在过去200,000年内都没有灭亡~
由此我们可以做一些性质上的探索。
1. 把这个紫色的概率条放在整个时间轴的最右端的话,可以发现根据哥白尼原理,如果一个事件(比如柏林墙的倒塌)在过去N年都没有发生的话,那么他在接下来的前n年发生的概率是 n / (n + N)。这看上去是一个很有规律的分布,似乎可以由平均分布(哥白尼原理的基础)由某种经典的推导得到,就像大数定理的证明那样…不确定,但感觉可能挺美…
2. 仍然来看柏林墙倒塌这件事,可以发现柏林墙在以下年份间倒塌的概率都是50%:
24.000000 2.666667
25.333333 2.810811
26.782609 2.958904
28.363636 3.111111
30.095238 3.267606
32.000000 3.428571
34.105263 3.594203
36.444444 3.764706
39.058824 3.940299
42.000000 4.121212
45.333333 4.307692
49.142857 4.500000
53.538462 4.698413
58.666667 4.903226
64.727273 5.114754
72.000000 5.333333
随着年份的推移,它们的差值越来越大。
好像没有得到什么有意义的结论比如对错之类…但感觉挺有意思的:-)
不明白,,请谁帮忙解释一下
”
若我出生在第二行的Now位置,人类文明将持续7.8百万年;而若我出生在第三行的Now位置,则人类文明只剩下5100年。
”
7.8百万年和5100年是怎么来的?
说白了,这个家伙就是胡来的。
这就是Doomsday Argument.
http://en.wikipedia.org/wiki/Doomsday_argument
他忽略了人口增长…… 由于人口越来越多,now 位置的概率分布就是不均匀的…… 也就是哥白尼原理不适用(每个时刻并非平权的) 所以有问题呀有问题……
这个应该算是时序分析,即每一个时间点对未来任何一点都有影响,因此不能使用古典概率这个假设,就像
hawk says:
March 17, 2010 at 12:01 am
我觉得问题在于他有一个假设那就是人类或者柏林墙倒塌或者whatever在任意未来时间倒塌的可能性是相等的。
真不错哈。
既不在特殊的时间,也不在特殊的位置。
由这句话推导出的结论,也被这句话所摧毁。
“人类有95%的概率在xxx年到xxx年灭亡”,
暗示关我们有理由相信我们落在95%的区间了,
这个“暗示”的“有理由的相信”,就过于特殊了。
如果没理由相信,结论又没意义了。
说得不太清楚,我只是想表达这个推理的漏洞在于逻辑与语义的模糊。
50%,95%怎么来的?
他是已经有了答案,然后利用答案去推导答案。
这推导完全建立在哥白尼原理的基础上,牺牲了估计的准确性从而得到估计值,这点想法很有趣!如果我们选取估计准确性为100%,那么容易算得没发生的事件在从现在开始到无穷未来发生的概率为100%,这等于废话:它在过去没有发生,于是在未来发生。
然而,哥白尼原理一定正确吗?或许使我们还没找到反例。
嘿嘿,这是一种概率游戏。概率本质上是信息量的反映。
我们增加一个假设,可以得到有利于2012人类灭亡的概率结论:
我们假定Dr. Gott是第一个想出这种预测算法的人。那么,由哥白尼原理,今天我“用这种算法来预测人类灭亡时间”这件事发生的时间可以认为是均匀分布在“Gott想出这个算法那天”到“人类灭亡”这段时间内。于是算法的初始输入就由200,000变成了20(或更小),结论是人类文明在0.51~780年内灭亡的概率是95%,在20/3 ~ 60 年内灭亡的概率是50%
既然他没有用到任何信息,那么这一结论不包含任何信息:你在推导时就假设了文明存在必然有其终点,那么结论也告诉你文明有一个终点。既然你在推导时就已经假设文明的起点、终点和你的存在服从一个均匀分布,那么这个让你觉得很神奇的区间,不过是概率的一个把戏。可以想见,如果你把预测的概率推至无穷大,那么文明的终点也就无穷远。
这个结论唯一的用处是:使用两个假设(有起始,有分布)将一个时间概念转变成了概率的概念。
第一次来这里
这是一种不同的思维方式 感觉很诡异 但很能引起联想
作者的推导是有了结论,然后再推导的。
比如说,你都已经知道柏林墙生存的周期了,你还推什么百分比,什么时候倒?
下面推测人类历史,你知道人类历史的200000年是多少百分比,那就是直接都知道人类文明的长度了?
你怎么知道你访问的时间是Now那个位置?你又如何知道这个NOW是25%????????
我认为你没有看懂。
我认为这种推理方法,从统计意义上来说是完全正确的。只是假设人的出现时刻在时间上均匀分布太简单了,不过对于人类这么漫长的历史来说,可以近似为均匀分布。另外如果只求单侧区间,可以以相同的置信度得到更低的上限值,比如,可以算出,人类在380万年灭亡的概率是95%。
作者在25%处访问柏林墙后0-25%的可能性已经是0了
忽略人口的变化,倘若能从我们所在的点出发,对由此开始分支的无数平行宇宙观测,也许会得到95%的概率在某一区间。然而概率对频率的估计事件是对大量重复事件而言的。而我们所能经历的历史有唯一性
这个难道不应该是把所有历史上出现的人的结论综合(平均(甚至加权平均,鉴于人口分布本身就不均匀))之后才是有效的预测么?
有个问题:推导有个前提,就是作者假定访问柏林墙只访问了一次,将来不会再访问,所以才知道是均匀分布。但是在作者第一次访问柏林墙时并没有理由认为这是历史上唯一一次访问柏林墙。这点我觉得想不通。