细推物理须行乐 何用浮名绊此身
Search
-
Recent Posts
Random Posts
Tags
Links
很久以前看过求平方根的这么一个方法,是用的迭代,按下面这个公式进行迭代即可求出a的平方根:
Xn=(Xn-1+a/Xn-1)/2 (n>0)
其中X0可以随便取一个数。当Xn-Xn-1满足精度要求时,即可输出Xn作为答案。
很长时间以来都想不明白,为什么通过这样的迭代会算出平方根。上网查他的原理也没查到。最近在《边缘奇迹——相变与临界》上看到了重正化群中类似的东西,我恍然大悟,想到了怎样来理解。
我们画出y=(x+a/x)/2的图像,再在同一坐标系内画出y=x。如下图(a=2):
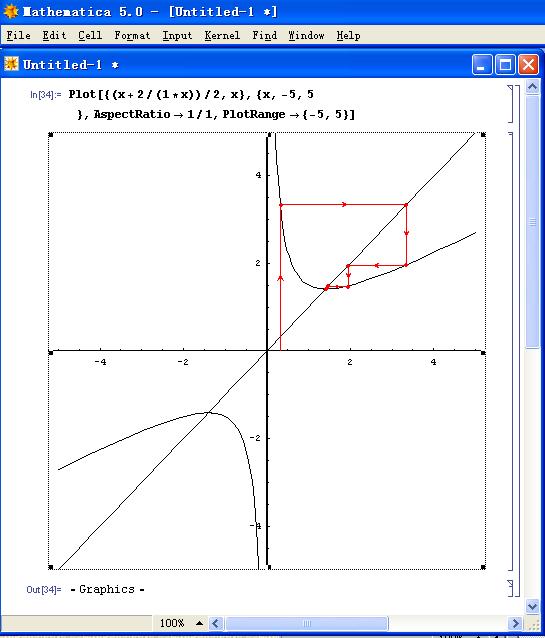
随便取一个X0,做竖直直线,找到他与y=(x+a/x)/2的交点,交点的纵坐标即为X1。再过交点做水平直线,找到与y=x的交点,其横坐标即X1。再过交点做竖直线,找到他与y=(x+a/x)/2的交点,交点纵坐标即为X2。再过交点做水平直线,找到与y=x的交点,其横坐标即X2……不停地做下去,通过图就可以看出交点逐渐逼近两条函数曲线的交点,即点(√2,√2)。
一般的a也是一样,最终逼近于(√a,√a)。
不过,我还是不知道这个迭代式是怎么找到的,我尝试过写出求三次方根的迭代式,结果无功而返。
上面的均属个人见解,如有错误请指出。
physixfan
eaglefantasy
Eagle_Fantasy
宇宙的心弦
Traction Theme by The Theme Foundry
Copyright © 2025 physixfan. All rights reserved.  宇宙的心弦 by physixfan is licensed under a Creative Commons Attribution-NonCommercial-NoDerivatives 4.0 International License.
宇宙的心弦 by physixfan is licensed under a Creative Commons Attribution-NonCommercial-NoDerivatives 4.0 International License.
Necessary cookies are absolutely essential for the website to function properly. This category only includes cookies that ensures basic functionalities and security features of the website. These cookies do not store any personal information.
Any cookies that may not be particularly necessary for the website to function and is used specifically to collect user personal data via analytics, ads, other embedded contents are termed as non-necessary cookies. It is mandatory to procure user consent prior to running these cookies on your website.

这个应该是有牛顿切线法的结果吧……
y = x^2 – a = 0 的解法:
任取 X(0)>0 ,Y(n) = X(n)^2 – a,
相应的切线与 X 轴的交点 X(n+1) 满足
(X(n)^2 – a)/(X(n) – X(n+1)) = 2 * X(n) = y'(X(n))
解这个方程,X(n+1) = (X(n) + a / X(n)) / 2
相似的,求 a 的 m 次方根的迭代式应该是:
X(n+1) = ((m-1) * X + a / X^(m-1)) / 3
应该是重整化群利用了不动点的知识,而不是不动点利用重整化群的知识,你现在大几了?知道的东西真不少
我是高三的…
我只是看到了那本书上的一点关于重整化群的东西,对它并不清楚
姑娘, 这个是牛顿迭代公式的变形;理解复杂化了
我知道如果把一无理数平方根化成以1为分子的连分数,那么这个连分数的分母是循环的。进一步可以退出一个迭代公式,可以进行逐步提高精度的迭代计算。
这就是不动点嘛
原来你现在是博士!
评论里的大佬们打开了我的眼界,感恩数学,感恩简单易懂的博客!