小游戏“围住神经猫”背后的数学问题

一夜之间,微信朋友圈便被这个有趣的小游戏“围住神经猫”刷屏了。如果没有见过的可以点开这个链接玩玩看:围住神经猫。一开始看到刷屏的小游戏,我不以为意,以为又是一个无聊的游戏罢了,但是当进去玩了一次之后,便恍然大悟为什么它会火了:这不就是数学游戏界神人John Conway设计的“天使与魔鬼”游戏么!John Comway最有名的数学游戏作品大概是“生命游戏”了,其规则之简单和产生的变化之丰富多彩实在是让人叹为观止;另外著名的“自由意志定理”也出自他的手中。这次的“天使与魔鬼”游戏,于1982年发表,也是他的作品中极其有趣的一个。
最原始的“天使与魔鬼”游戏规则是这样的:在无限大的2维正方形格点上,两个玩家,分别称为天使和魔鬼,轮流行动。初始时,格点是空的,只有天使站在棋盘的原点处。魔鬼每轮的行动是可以在天使站立的格点之外的任意一个格点处挖一个陷阱,挖好的陷阱会始终存在在棋盘上;天使每轮的行动是可以每次移动至多k步,其中每一步可以是横向、竖向或者斜向走一格,k为正整数。下图为示意图,红色是魔鬼挖好的陷阱,而蓝色虚线框表示k=3时天使一次行动可以到达的范围。天使行动时可以跨过陷阱,但是不可以踩在陷阱上。最终,如果天使被围困得无论如何也不得不踩在陷阱上,魔鬼就赢了;如果天使可以无限地逃跑,天使就赢了。问题是:k等于几的时候魔鬼有必胜策略,等于几的时候天使就有必胜策略了?…
钝角其实和直角相等!我们的教科书真实率低于5%,连数学也不例外。
“我们的教科书真实率低于5%,连数学也不例外,年轻人要敢于怀疑。越是从小学习,看起来理所当然的知识越值得怀疑。钝角其实等于直……”1968年冬天,在刺骨的寒风中,数学教授赵文武凛然站在后海的岸边,最后一句尚未说完,便被疯狂的红卫兵挂上石头沉入了后海。
在我们的少年时代,有很多人都有这样的经历,在各种平面几何问题中抓耳挠腮,证明来证明去,为了证明一个角是直角而浪费了精力,荒废了青春。很多人因为不会证明平面几何中关于直角的问题,遭到父母的毒打,乃至与梦中的重点中学、大学失之交臂。可又有多少人知道,其实钝角就等于直角。所有钝角尽管看起来不一样大,但是早在欧几里得时代,伟大的古希腊数学家们就早已通过严格的数学证明了钝角统统等于直角!可是在中国,黑暗的中国教育界却可耻的隐藏了这一秘密,当今中国几乎就没有人知道钝角和直角相等这一本该人尽皆知的秘密!
众所周知,平面几何的最经典著作当属欧几里得的《几何原本》,当今所有的平面几何课本都基本按照原本的框架讲述。而关于钝角等于直角的证明,其实就静悄悄的隐藏在《几何原本》的后记当中。下面贴出古希腊数学家给出的证明:
盘点数学里十大不需要语言的证明
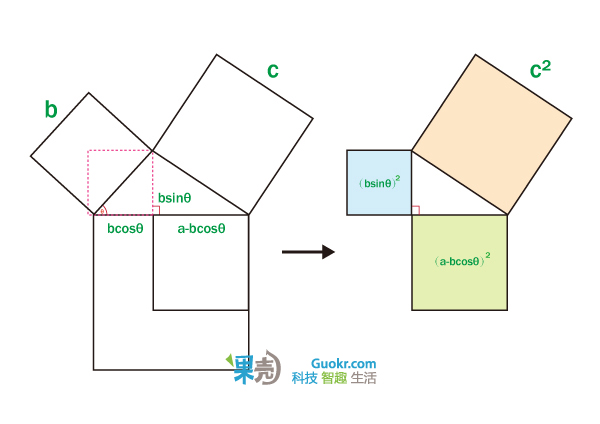
0. 勾股定理&余弦定理
这个大家小学就学过的古老定理,有着无数传奇故事。我可以很随意的写出她的10个不同的证明方法。而路明思(Elisha Scott Loomis)在 《毕达哥拉斯命题》( Pythagorean Proposition)提到这个定理的证明方式居然有367种之多,实在让人惊讶。这里给出一个不需要语言的证明方法。

实际上勾股定理是余弦定理的一种特殊情况,而余弦定理的证明,同样可以不用语言。
1. 关于反正切的恒等式
…e,一个常数的传奇
自然对数的底e是一个令人不可思议的常数,一个由lim (1+1/n) n 定义出的常数,居然在数学和物理中频频出现,简直可以说是无处不在。这实在是让我们不得不敬畏这神奇的数学世界。
欧拉恒等式
但凡说起e,一个必定要提到的公式就是欧拉恒等式——被誉为世界上最美丽的公式。
$$e^{\pi i}+1=0$$
数学中最基本的5个常数——0、1、圆周率π、自然对数的底e和虚数单位i,以及数学中最基本的两个符号,等号和加号,就这样通过一个简单的恒等式联系在了一起,实在是让人叹服。
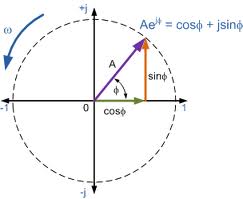
这个等式有个一几何的直观解释。一个实数在实数轴上可以用一个向量表示,旋转这个向量,就相当于乘以一个虚数i。据此建立一个以实数为横轴,虚数为纵轴的坐标系。实单位向量,每次逆时针旋转π/2, 可以分别得到结果1,i,-1,-i,1. 即转4次以后就回到了原位。而当实单位向量保持长度不变旋转θ角度,得到的向量就是:cosθ+isinθ。根据欧拉公式 e iθ = cosθ+isinθ可以看出 e iθ 就代表实单位向量1旋转θ角后而得到的向量。所以 e iπ 意味着单位向量逆时针旋转了π,结果显然是-1。
增长规律
这个世界上有许许多多的事物满足这样的变化规律:增长率正比于变量自身的大小。例如放射性元素衰变的时候,衰变率就和现存的放射性物质多少成正比;资源无穷多的社会,人口出生率将(近似的)和现存人口数成正比等等。而此类变化规律所确定的解,则是由以e为底的指数增长所描述的:如果x的变化率等于变量x自身的λ倍,那么该变量随时间t的函数则为
$$x=Ce^{\lambda t}$$(C是任意常数)
而e的直观含义正是增长的极限,这个问题在 数学常数e的含义 中有过详细的介绍。
正态分布
…代数基本定理的一个最简单证明
//看懂本文需要且仅需要关于复数的基本概念。
代数基本定理,是指任何一个一元复系数多项式都至少有一个复数根。从代数基本定理可以很显然的推论出我们可能在初中就已经熟悉的一个结论:一元n次方程必有n个根。虽然大家都已经对这个定理感到习以为常,但是其实它并不是显然的,因为如果只考虑实数,一元n次方程就不一定有根。当把研究对象拓展到复数时,一下子所有代数方程就有解了,这其实是一件很不显然的美妙结论。
关于代数基本定理,有很多很多种证明方法。貌似第一个证明是牛逼哄哄的高斯在博士论文中给出的…基本所有的证明方法都或多或少的用到了一些比较高等的数学,对于只有高中数学知识的人来说很难看懂。即使是《什么是数学》里给出的证明,也用到了一个并不是那么好理解的“卷绕数”的概念。但是,下面要给出的证明,只需要有关于复数的基本概念就可以理解,只要几句话就证明完毕了!此证明由北大数院的范后宏老师在“古今数学思想”课上提供。
代数基本定理证明:
设$$w(z)=z^n+a_{n-1}z^{n-1}+…+a_0$$
于是我们想要证明的结论就是:一定能找到某个z,使得w(z)=0。
我们先把z写成$$z=re^{i\theta}$$的形式。
首先,我们考虑r=0的情况。这时w(0)将是复平面上的一个点,并且这个点就是a0,且a0不等于0。(如果a0等于0那z=0就是原方程的解了,定理直接得证。)
然后,我们再考虑0<r<∞的情况。对于一个固定的r,如果这时我们让θ从0到2π连续变化,那么对应着w(z)将会在复平面上画出一条封闭的曲线,如下图。这个曲线可能是很扭曲的形状,也不一定是绕了一圈的,可能绕了很多圈。比如w(z)=z^2,当z的辐角从0到2π连续变化时,w(z)将在复平面上绕着一个圆转两圈。在这里我们并不关心这条曲线的具体形状。
最后,我们再考虑r->∞的情况。此时当z的辐角从2π连续变化时,显然w(∞)的所有值都将是无穷大(因为此时只有z的最高阶项是起作用的,而它前面的系数是1),对应着就是w(∞)将在复平面上的无穷远处画出一条封闭曲线,见下图。…
赌场是凭借这个方法赚钱的吗?
众所周知,去赌场赌博,赢钱的一定是庄家。通过概率的不均等让你赔钱你肯定陪得心服口服,但是有人提出了这样一种赌场赚钱的方法,即使是输赢概率为1/2赌场也会赚钱,乍看起来似乎确实有道理:
就假设赌徒跟赌场玩的是赌大小的问题,输赢概率是严格的1/2。赌徒身上带着5元钱,每次下注1元。如果赌徒身上的钱在某个时刻输光了,那么赌徒就会离开赌场回家;如果赌徒连续赌了1000次都没有输光,赌徒在这个时刻就会停止赌博结算完毕回家去。如此一来,利用赌徒停止赌博两个边界条件的不对称性,随着赌徒增多,赌场就可以从中赚钱了~!
乍看似乎确实有道理,因为不仔细想的话会觉得赌徒输钱离开赌场的概率似乎确实比较大。但是如果写一个程序跑一跑看看赌场最终会赚多少钱,结果会出乎意料:赌场赚到的钱数将会在基本上以0为中心的一个范围内震荡,并不会随着赌徒人数增多而增多!
问题出在哪呢?其实这个结果也不算过于出乎意料。因为虽然赌徒输钱离开的概率是比较大的,但是他赔的钱就那么些;但是赌徒如果是赌了1000次才离开的,走的时候赚走的钱数可能相比而言是很多的。于是二者的作用是有可能恰好抵消的。如果你有耐心做详细的定量数学计算的话,其实是可以解析的给出这个问题的结果的,赌场赚到的钱数随赌徒人数怎么变化是可以精确算出来的。
但是还有一种很巧妙地思路可以一下子看出来,其实赌场从期望上来说就是不赚的!仔细想一下:…


