拈游戏
所谓拈游戏的规则是这样的:(在看了沙发的评论之后我才知道其标准名字应该是Nim游戏…)
桌面上有三行硬币,每一行中分别有a1、a2、a3个硬币,其中a1、a2、a3是可以任意指定的正整数。两个人轮流拿走硬币,每一次只能从某一行中拿走任意多个硬币,谁拿走最后一枚硬币谁就赢了。
比如说a1=1,a2=2,a3=3的情况吧,这时如果轮到我拿了,我可以从第三行拿走2枚硬币,或者可以把第三行的三枚硬币全都拿走,等等;但是我不能同时从第一行和第三行里各拿走1枚硬币。这个简单的情况,可以枚举所有可能性得出结论:先拿的必输。
当a1、a2、a3是任意给定的,在什么情况下先拿的必输呢?必胜策略是怎样的呢?这是一个相当有意思的问题,答案可绝不是显而易见一目了然的。而当我当年看到这个策略长什么模样之后,完全的叹服了。今天我就先不写必胜策略了,大家可以先自己想想,如果下周或者什么时候有时间了再来写。前一阵子我为了熟悉C++自己写了一个拈游戏的人机对弈程序,大家可以点击下面的链接下载。其中包含了必胜策略,所以只要你一步走错就一定会输。
其实拈游戏不仅仅局限于三行硬币,其实最初的问题是N行的,而且神奇的是其必胜策略对于任何N都是一样的。其实这个拈游戏是我上小学的时候奥数老师跟我玩的游戏,最近才发现这个经典的有意思的游戏还有好多人没有玩过,故写此文……
猫捉老鼠问题
这个是我室友的力学老师留给他们的思考题,因为它完全符合思维过程相当困难、但是解答却极为漂亮简单的原则,所以我就转过来分享一下。
在数轴上,0的位置停着一个不动的老鼠,1的位置在初始时刻有一只猫。猫是可以走动的,每一步在数轴上分别以二分之一的概率或朝着正方向或朝着负方向走1的距离。当猫到达0的位置时,猫就抓到老鼠了,游戏结束。问当猫走的步数趋向于无穷大的时候,最终捉到老鼠的概率是多大?一定要先仔细思考再看解答……
直上九宵的指数方程
有一道很简单的小问题:求解方程
$$\Large x^{x^{x^{x^{…}}}}=2$$
这样的方程解起来是很简单的,因为最低下的x的指数是他本身,即它的指数是2,因此该方程等价于x^2=2,立刻解得x=√2。
但是,如果题目地形式稍微一变,变成这个样子:
$$\Large x^{x^{x^{x^{…}}}}=4$$
用同样的方法你将会得出同样的答案x=√2。
现在问题来了,既然如此,那么表达式
$$\Large \sqrt 2^{\sqrt 2^{\sqrt 2^{\sqrt 2^{…}}}}$$
到底等于几呢?2还是4?…
有趣的无规行走模型
昨天和一帮子同学出去玩,晚饭时间点完菜等待上菜的时候有两个同学玩起了一个非常无聊的游戏:甲同学扔硬币,乙同学猜正反面,如果乙猜对了则乙的鼻子变长1cm,反之如果乙猜错了则鼻子缩短1cm。(这个是和谐过的版本,原始版本变长变短的不是鼻子而是另一个猥琐的东西…)。他们正在无聊的玩,全然不知道这么玩下去他鼻子长度的绝对值期望是多少…其实,这正是我高一的时候在费恩曼物理学讲义上看到的一个数学模型:Random Walk(无规行走)。对于这个模型,我敢说绝大多数人凭直觉会觉得鼻子长度的绝对值最终的期望值会是0,但事实绝非如此,你可以自己扔几次硬币试试,正确的答案应该是你扔硬币次数N的平方根!
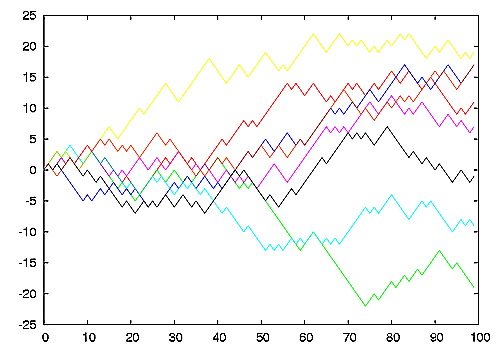
下面给出证明,该证明基本来自《费恩曼物理学讲义》第一卷:…
几个数学娱乐
今天六一,这个曾经属于我们的节日。岁月无情的在我日渐苍老的脸上刻上了印记,看到照片上小时候稚嫩的我,看到肯德基里面孩子们无忧无虑欢乐的笑脸,我总有种莫名的感伤。今天写下几句小的数学娱乐,来祭奠逝去的似水年华。虽然我们不能企图永远年轻,但至少可以像小孩子那样笑颜永驻。
1.我已经证明了著名的数学难题:任何一个偶素数总能写成两个奇数之和。
2.对于这个数学难题:方程n^a+n^b=n^c对于n>2没有正整数解,我已经找到了一个极其简单的证明,甚至一页之内就能搞定。
3.我已经想到了一个绝妙的宇宙万能公式,只不过这里空白太小,写不下…(这句话曾经是我的校内网状态和QQ个性签名,用在有字数限制的地方特别合适)
4.原来任何进制都是10进制..
5.世界上有10种人,一种是懂二进制并且看贴回贴的人,一种是不懂二进制或者看贴不回帖的人……
《哥德尔 埃舍尔 巴赫——集异璧之大成》
最近正在家拜读传说中的旷世奇书《哥德尔 埃舍尔 巴赫——集异璧之大成》。当我刚刚看完第一章的时候就已经完全被这本书给镇住了,而且越往下读越被这本书深深的震撼。读这本空前的奇书带给我的精神上的愉悦感甚至要大于跟美女聊天…
哥德尔Godel是伟大的数学家(参见这篇文章),埃舍尔Escher是诡异的画家(参见这篇文章),巴赫Bach是人尽皆知的音乐家。《集异璧之大成》这本书讲了这三个人,三个完全不同的领域,结果你会发现这三个领域不仅仅是具有深刻联系,而且甚至可以说他们是一个统一体的三个不同侧面!英文版的封面画(下图)很好的反映了这一点。
 …
…


