什么是直线?
什么是直线?或者更加准确的问法是如何定义直线?不知道你有没有思考过这个问题。尽管我们实际生活中都有对直线概念的直观理解,但是考虑到后来非欧几何的问世,我们理应对直线有一个更深刻的认识。
欧几里得的几何原本上是这么定义直线的:“直线是它上面的点一样地平放着的线”,其中线的定义是“线只有长度而没有宽度”。显然在逻辑上这样的定义是极其不严格的,因为什么叫做“一样的平放着”只是一个日常生活中的直观概念。这也就是说欧几里得的几何原本相当于并没有对直线给出定义,尽管直线是几何学最基本的基本概念之一。
可能很多人会认为直线被定义成“两点间最短的线”(在这里就不去区分线段和直线了),然后就觉得在逻辑上就已经定义清楚了。但是这里还有一个问题,那就是什么叫做短?要有长短的概念就要先有距离的概念,而仅仅在几何学内考虑这个问题的话,要丈量距离就必须先有尺,而尺的形状又是直的,因此距离的概念其实是建立在直线的概念之上的。所以如果只考虑几何学那么用距离定义直线就成了循环定义了。
所以在数学上,我们就不能单从几何的角度去定义距离了。为了定义距离,我们需要在空间的每一个无穷小的区域上建立一个笛卡尔坐标系,在每一个小的笛卡尔坐标系内部可以通过普通的解析几何的方法定义出距离,然后在整个路径上对每一个小段上的距离进行叠加,从而定义出两点间连线的距离。之所以能在无穷小区域上建立笛卡尔坐标系,是因为一条曲线在无穷小区域上,我们可以把它近似为一小段直线(这个直线就是我们通常直观认识的直线),这个思想其实在最基础的微积分里面就已经有了。(如果一个空间奇异到在无穷小区域上无法建立笛卡尔坐标系,那么一般我们就不去研究它了。)至于为什么不能直接在大区域上直接建立笛卡尔坐标系来定义距离,原因很简单,坐标轴要画成直线啊,在没有直线概念的时候又哪里来的坐标轴呢…一个能够帮助理解的简单例子是在球面上定义最短线,如果直接建立笛卡尔坐标,其中的坐标轴就用我们直观感受的那种直线的话,那么最短线是必须脱离球面而经过球面之外的空间的。但是在球的表面的每一个无穷小区域上建立微小笛卡尔坐标系,就可以很好的沿着球表面定义出一条最短线。
至此,我们基本上可以把直线就定义成两点间距离最短的线了。但是,一定要知道一点,如此定义并没有定义出唯一一种直线。显然在一个球面上定义出的最短线,在我们看来其实是圆弧;在马鞍面上画出的最短线,在我们看来也是弯弯曲曲的线…他们都属于非欧几何。庞加莱圆盘模型(参见这篇文章)就是非欧几何的一种,按照那里定义的距离,圆盘模型内的直线在我们看来就成了圆弧了。
那么怎么定义才能保证刚才定义出来的直线就是我们通常直观上的直线呢?其实很简单,只要再加上一个公理,即传说中的欧几里得第五公设就可以实现:同一平面内一条线段和另外两条线段相交,若在某一侧的两个内角的和小于两直角,则这两线段经充分延长后在这一侧相交。非欧几何正是做出了与第五公设相反的假设而得名的,给出不同的公理,就会得出各种各样的非欧几何。
至此,我们终于可以引入Hilbert大神对直线的理解了:…
辛普森悖论:诡异的男女比例
大学的男女比例问题一直是广大宅男同胞所关心的重大问题,也是高中同学聚会时必然谈起的话题,对于选择大学来说,这也是一项重要指标~..
一天,我拿出两个大学(P大和T大)的统计数据开始研究。“物理学院,P大男女比例大于T大;数学科学学院,P大男女比例又是大于T大…哇,怎么所有专业P大的男女比例都高于T大啊…那还犹豫什么呢,我肯定报T大了!”正当我刚刚心意已定的时候,突然看到了统计数据的最后一行:P大的总体男女比例低于T大!“什么?!有没有搞错?怎么可能P大的所有专业男女比例都高于T大,但是整体男女比例却低于T大了呢?!肯定是哪里算错了吧…”于是我拿出计算器狂敲,却发现没有任何一个计算错了的数据,这种情况真的可能发生吗?
多说无益,请看下面编造出来的一份男女比例数据:(其中假设两所大学都只有物院和外院两个专业)
物院的数据:
| 男生人数 | 女生人数 | 男:女 | |
| P大 | 45 | 8 | 5.6:1(大) |
| T大 | 101 | 51 | 2.0:1 |
外院的数据:
| 男生人数 | 女生人数 | 男:女 | |
| P大 | 50 | 201 | 0.25:1(大) |
| T大 | 9 | 92 | 0.10:1 |
学校整体数据(即上述两个专业人数之和):
| 男生人数 | 女生人数 | 男:女 | |
| P大 | 95 | 209 | 0.45:1 |
| T大 | 110 | 143 | 0.77:1(大!) |
数据可不会是骗人的,不信可以自己动手验算一下,真的出现了这种违背常理的情况!这种现象被称为“辛普森悖论”,虽然这么叫,但其实这不是个真正的悖论,它内部没有包含逻辑上的矛盾,只是违背了人们的常理。…
复数方法巧解平面几何题
快放假了才买到《复分析——可视化方法》这本书,相见恨晚啊,这本神书,如果我能早点读,这学期的复变函数估计就学的不会这么吃力了。。。在这本书开头的地方有一个用复数方法解决平面几何问题的例子,我一看便惊了:这正是我初中时候见到的一道印象极其深刻的平面几何题,曾为它绞尽脑汁也没有想出做法呢,然而这本书就用复数的方法巧妙而自然给解决了~ 贴出来共享一下。
题是这样的:证明,在任意四边形的四条边上各做一个正方形,那么连接相对的正方形中心的线段互相垂直并且等长。示意图如下。
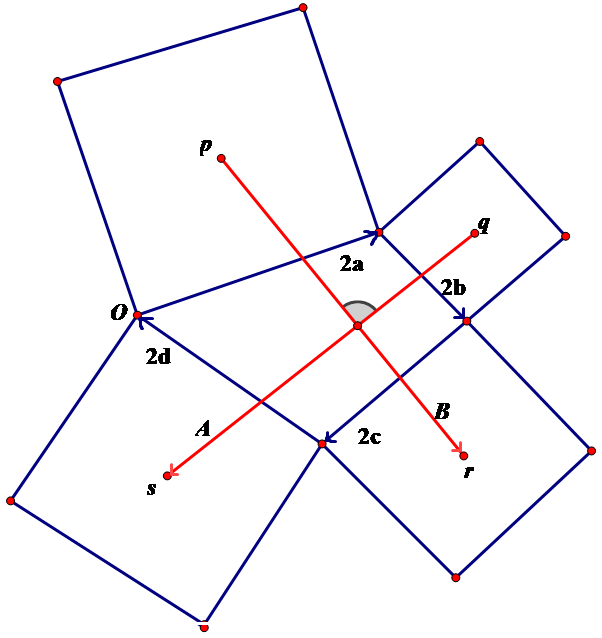 …
…
人的非理性选择
考虑这样一个情景:两个古董专家利用公款在国外买了一个珍贵的古董,但是他们回国的时候因为飞机的托运,把古董给摔坏了。航空公司决定赔偿,但是古董这种东西,价钱可不好衡量,万一他们漫天要价航空公司也不好辨别,于是他们就想出了一个招:把这两个专家隔离开来,分别问他们这个古董的价格,然后按照两个价格中较低的那个进行赔偿,同时再付给报低价的那个人同样多的钱(如果两人报价相同就只照价赔偿而不另外付钱)。//注:额外给的钱是奖励给个人的奖金,你并不能指望你的同事拿到这笔钱之后跟你平分…
这一招可够狠的,如果这个古董的价格在两位专家心里都是1万美元,他们会如何报价呢?A会想,如果B如实报了1万美元,那我报9999美元,就可以净赚很多。可是,转念一想,如果B想到了我会报9999元,而报9998元怎么办?那么我的对策就是,我说9997元..可是,如果B连这一步也想到了怎么办…如此下去,想的越深,报价就会越低,如果按照经济学中的理性人假设的话,如此分析下去,两个人只有都报0元才能最终达到纳什均衡,而这个结果却正是最坏的结果。
那么在实际中遇到类似情况大家会怎么报价呢?
这让我想起了在学而时嘻之看到的一个案例。《金融时报》刊登了一个很诡异的广告,说你可以随便写一个0~100之间的整数寄回编辑部,然后如果你写的这个数最接近所有寄来的数的平均数的2/3,你就可以获得一张伦敦到纽约的头等舱往返机票。
如果是你你会写几呢?…
上帝能造出他自己都搬不动的石头吗?
小时候看《时间简史》,对里面一副插图里的话印象很深:“上帝能造出他自己都搬不动的石头吗?”,从此我便把它作为上帝不是万能的这一命题的证明。因为,如果你回答“能”的话,那么上帝就连某块石头都搬不动;而如果你回答“不能”的话,那么上帝就连一块满足某条性质的石头都造不出来,他也不是万能的。
但是,其实这个证明里面隐藏着一个致命的逻辑错误。
这要从如何定义一个概念说起。在逻辑学上,对于定义有一条不起眼的要求,那就是给出定义以后要证明其存在性。比如说我定义质数为除了1和它本身没有其他正约数的正整数,从理论上来说我得证明这种数是存在的,我们可以举个例子来证明其存在性,比如说2就是质数。这可能和我们这么多年的学习经验不符,我们学习数学概念的时候可从来没有见过什么存在性证明啊…我们学的大多数概念的存在性的证明都是比较显然(举个例子就可以了),因此在课本里从来不出现,但是这绝不意味着存在性证明没有用,尤其在抠逻辑漏洞的时候。
比如说吧,我要定义一种数叫做“蛋疼数”,他被定义为“大于2的偶质数”,显然蛋疼数就不存在。然后假如我基于蛋疼数演绎出来了一整套蛋疼理论,看上去完美无缺而且非常漂亮,可是回过头来一看,哎呀,蛋疼数居然不存在,那整个理论体系的根基就倒塌了。
再比如说,我要定义一种数叫做“牛逼数”,他被定义为“大于4的不能写成两个质数之和的偶数”,很明显牛逼数就是违反哥德巴赫猜想的数…这样,牛逼数的存在性证明实际上就是找到哥德巴赫猜想的反例,这可实在不是一件很显然的事情…
好了,回到上帝是不是万能的问题上来。…
神秘的本福特定律
统计一下世界上237个国家的人口数量,你觉得其中以1开头的数会占多大比例,而以9开头的数又占多大比例呢?如果你的回答是都为1/9,恭喜你你是正常人,但是事实却不是如此:以1开头的数惊人的占到了27%,而以9开头的数却只占5%。下图可以很形象的展示出在各国人口数量问题上,以各个数字开头的数占了多大的比例(图片来自维基百科)。为什么会相差这么大呢?这正是神秘的本福特定律在起作用。
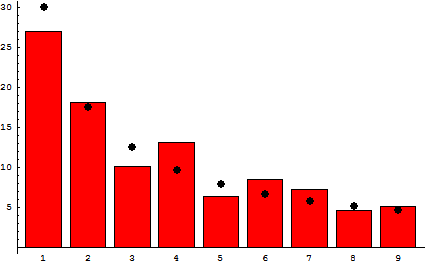
本福特定律,也称为本福德法则,说明一堆从实际生活得出的数据中,以1为首位数字的数的出现机率约为总数的三成,接近期望值1/9的3倍,推广来说,越大的数字,以它为首几位的数出现的机率就越低;精确地数学表述为:在b进位制中,以数n起头的数出现的机率为logb(n + 1) − logb(n)。
在十进制中,首位数字出现的概率为:
| d | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
| p | 30.1% | 17.6% | 12.5% | 9.7% | 7.9% | 6.7% | 5.8% | 5.1% | 4.6% |


