神秘的本福特定律

统计一下世界上237个国家的人口数量，你觉得其中以1开头的数会占多大比例，而以9开头的数又占多大比例呢？如果你的回答是都为1/9，恭喜你你是正常人，但是事实却不是如此：以1开头的数惊人的占到了27%，而以9开头的数却只占5%。下图可以很形象的展示出在各国人口数量问题上，以各个数字开头的数占了多大的比例（图片来自维基百科）。为什么会相差这么大呢？这正是神秘的本福特定律在起作用。

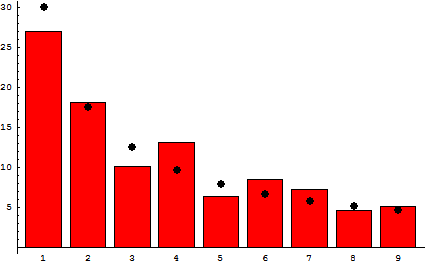
本福特定律，也称为本福德法则，说明一堆从实际生活得出的数据中，以1为首位数字的数的出现机率约为总数的三成，接近期望值1/9的3倍，推广来说，越大的数字，以它为首几位的数出现的机率就越低；精确地数学表述为：在b进位制中，以数n起头的数出现的机率为logb(n + 1) − logb(n)。

在十进制中，首位数字出现的概率为：

一个与直觉相悖的概率问题及其引发的严肃思考

一人用颤抖的双手拿着艾滋病检测呈阳性的化验单去找医生：

“医生，弱弱的问一句，这个检测呈阳性是什么意思啊？”

医生：“同志，做好心理准备，你很有可能要悲剧了…目前艾滋病在世界上比较严重，粗略估计大概每1000人中就有一人得艾滋病。我们采用的是某种血液试验检测法用于检测身体中是否含有艾滋病病毒，这种方法相当精确，但也可能带来两种误诊。首先，他可能会让某些真有艾滋病的人得到阴性结果，称为假阴性，不过只有0.05的概率发生；其次，它还可能让某些没有艾滋病的人得到阳性结果，称为假阳性，不过只有0.01的概率会发生。根据这些数据，你差不多可以估计出来自己的囧况了…”

那人：“我X，哥悲剧了…”

OK虚拟的情境到此打住，我现在要问一个问题，请先不要计算，先尝试着用直觉给出一个答案：如果你就是这位哥，在艾滋病检检测呈阳性的条件下，你真的得了艾滋病的概率是多大呢？

请从下面ABC三个选项中选出与你的直觉最接近的：A.90%;  B.50%;  C.10%。…