为什么频繁交易的人大多数在股市上都赔钱了?一个有趣的小数学游戏也许可以解答
今天偶然读到了这篇文章,里面提到的一个简单的小数学游戏相当有意思。
假设有这么一家赌场提供了这么一个你可以玩无穷多次的游戏:扔一个硬币,若正面向上,则你的资产变成当下的 1.2 倍;若反面向上,则你的资产变成当下的 0.83 倍。你会选择玩这个游戏吗?
有两种分析这个游戏的方式。
第一种:不论我玩的时候的本金m是多少,玩下一次的时候,收益的期望总是 m*(1.2-1)*1/2+m*(0.83-1)*1/2。因为赢钱的时候赢 0.2 总是大于赔钱的时候赔 -0.17,所以期望总是正的,那就应该玩,而且要一直玩无限多次。
第二种:若一直玩下去,就会有赢有输,所以应该把 1.2 和 0.83 乘起来看是否大于1。结果是 1.2*0.83=0.996,小于1,因此久赌必输,不能玩。
这两种分析哪一种更有道理呢?大家可以先想想看。
我多年不学数学了,概率论早就忘光了,因此就写了个小代码来模拟一下如果玩这个游戏,会是什么结果。
import numpy as np import matplotlib.pyplot as plt P = 100 # Number of players N = 30000 # Total times played for one player win = 1.2 lose = 0.83 Num_of_winner = 0 Money_of_the_luckiest_winner = 0.0 for j in range(P): m = np.zeros(N) m[0] = 10000.0 for i in range(1,N): if np.random.randint(2): m[i] = m[i-1]*win else: m[i] = m[i-1]*lose if m[-1]>m[0]: Num_of_winner += 1 if m[-1]>Money_of_the_luckiest_winner: Money_of_the_luckiest_winner = m[-1] plt.plot(m) print(Num_of_winner) print(Money_of_the_luckiest_winner) plt.xlabel('Times played') plt.ylabel('Money') plt.show() |
import numpy as np import matplotlib.pyplot as plt P = 100 # Number of players N = 30000 # Total times played for one player win = 1.2 lose = 0.83 Num_of_winner = 0 Money_of_the_luckiest_winner = 0.0 for j in range(P): m = np.zeros(N) m[0] = 10000.0 for i in range(1,N): if np.random.randint(2): m[i] = m[i-1]*win else: m[i] = m[i-1]*lose if m[-1]>m[0]: Num_of_winner += 1 if m[-1]>Money_of_the_luckiest_winner: Money_of_the_luckiest_winner = m[-1] plt.plot(m) print(Num_of_winner) print(Money_of_the_luckiest_winner) plt.xlabel('Times played') plt.ylabel('Money') plt.show()
在上面这段代码中,我模拟了100个玩家,每人玩30000次这个游戏,看看他们最后的资产有多少。
结果很有意思:其中绝大多数玩家的资产都可算是归零了!
最后print出来的 Num_of_winner 是资产大于本金的人,因为有随机性,所以每次运行结果肯定不同,但大多时候都是100人中有2~3人最终赢钱了而已。
更有意思的是,最后print出来的100人里面最后资产最多的人最后到底有多少资产 Money_of_the_luckiest_winner,经常是8位数9位数的资产(本金是1万)!这绝对是个赢者通吃的游戏。
下面贴一下其中一次模拟的图,大家可以看看:
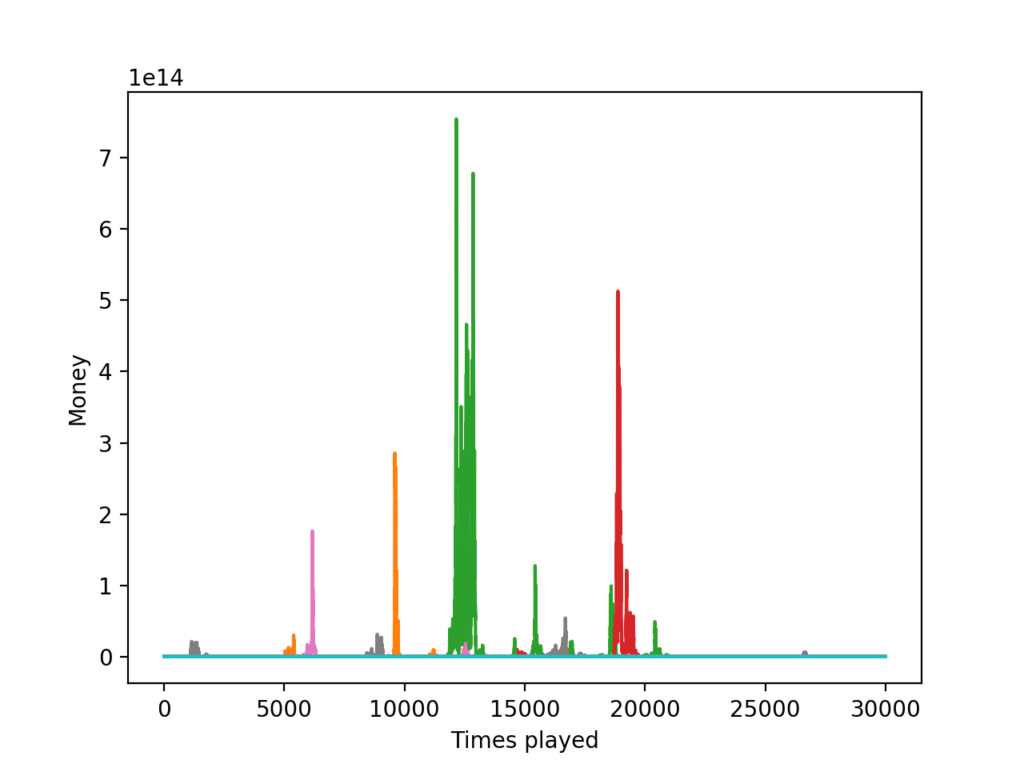
过程中纵坐标最高都到了10^13这个量级了,但最后的时候肯定没这么多。放大一下最后的结果,是这样的:
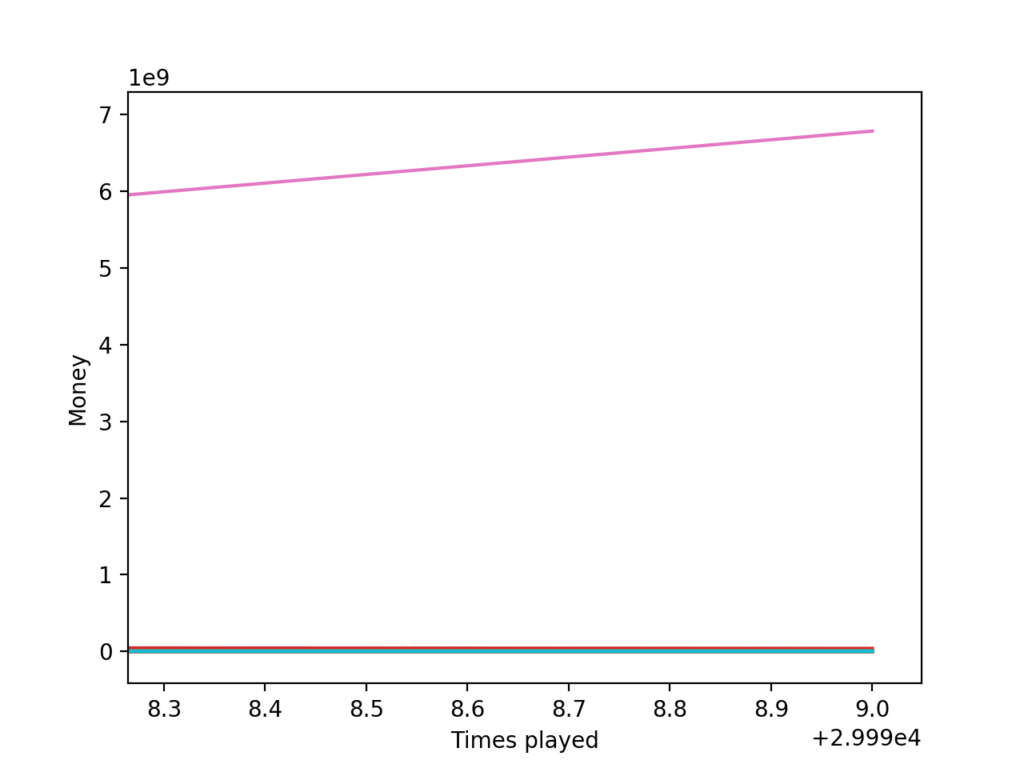
一个玩家遥遥领先,远远甩开了后面的其他所有玩家。
把最后的那一块继续放大,在排除掉了前4名之后总算纵坐标不需要用科学计数法了😂,剩下的玩家的资产都集中在0那里:
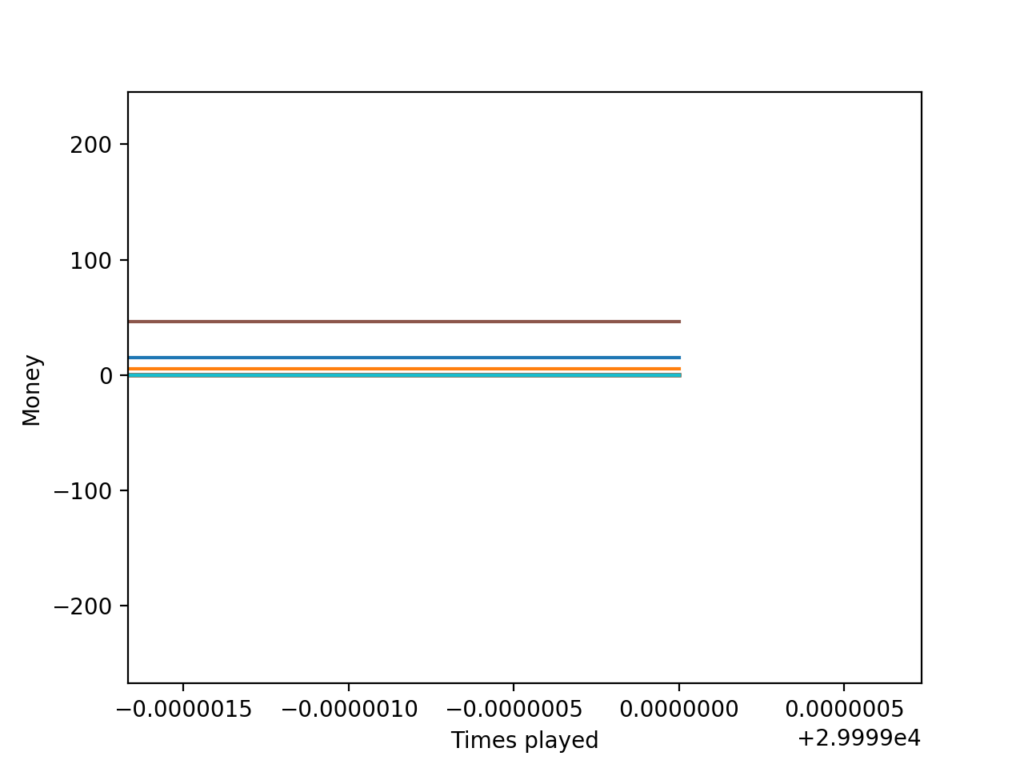
画一张纵坐标是对数坐标的图的话,可以更直观的看到大多数玩家资产向下的趋势(和上面几张不是同一个run):
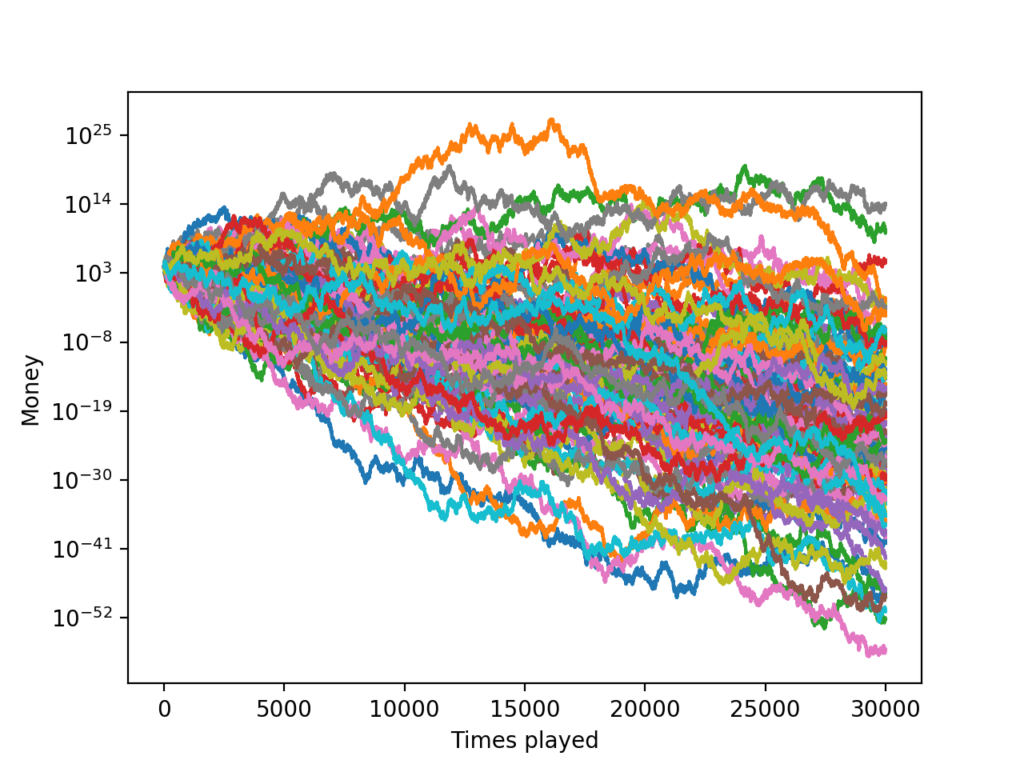
总结一下模拟的结果:绝大多数玩家玩到最后都归零了,只有极少数玩家能够赢得超过本金的钱,而赢得最多的那个人的最终资产远远超过其他人很多很多。
其实也不会有赌场提供这个游戏的,因为最一开始的第一种分析方式的确是没错的,玩家期望的确为正,赌场会赔钱。但第二种分析方式仍然有价值:只有1个人基本赢走了所有钱,剩下的人都归零了。
虽然没有赌场提供这个游戏,但是现实生活中,有一个地方跟这个小游戏太像了:股市!股市不是零和博弈,整体而言长期来看股市肯定是往上涨的,因为人类的生产力在提升。你买大盘指数基金buy&hold的话,期望肯定是正的。然而,股市每天都在涨涨跌跌,无数的人在里面频繁交易,最后血本无归。当然也有人最后成了大赢家,然而你能保证你是那个幸运的0.001%吗?
//知乎网友Richard Xu为本文中的小数学游戏提供了解析的分析,感兴趣的朋友们可以读一下:《“有趣的数学小游戏”背后的数学原理》。
//在写完这篇文章后,经过讨论又学到了有意思的东西,详见《用凯利判据玩转前文中的“一个有趣的小数学游戏”》。



有随机变量an, 为第n次赌博后本金与前一次的比值的对数。显然an以等概率取log(1.2) 和log(0.83)。根据中心极限定理,sum an 大约是一个高斯分布,其均值小于0。这样看的话,赌资exp(sum an)大部分情况小于本金,只有少部分情况是指数级大的。赌资大约是一个log normal distribution.
👍 有道理
n从30000换成3000,结论就大不相同。有>10%几率资产翻1000倍,我要玩😁
N->∞的结果才有意思嘛~
虽然期望值是正的,但从对数座标上来看,其实是关于本金的一维随机游走。已经证明了一维随机游走会无数次经过原点。而且钱这东西有最小单位,只要到 0 就 GG,哪怕期望再大,只要时间够长,一定会归零。
另外这玩意儿不是零和博弈,「绝大多数人都穷b,赢的人暴富」只能是个伪结论,巧合而已。