我发现的幻方小性质
正在看马丁•加德纳的书,忽然间想到了幻方,摆弄了一下居然发现了一个我以前没有看到过的性质,写下来和大家分享一下。
最著名的三阶幻方长这个模样:
| 4 | 9 | 2 |
| 3 | 5 | 7 |
| 8 | 1 | 6 |
现在用小键盘输入这9个数,顺序按照492357816这样。在小键盘的对应位置上写上每一个数字是第几个输入的,比如4是第1个输入的,就在小键盘4的位置写下1,9是第二个,在9的位置上应该写上2……这样一来小键盘上就写出了如下阵列:
| 6 | 7 | 2 |
| 1 | 5 | 9 |
| 8 | 3 | 4 |
这居然还是一个幻方,其实就是把上面那种幻方翻转了一下。
我又验证了一种四阶幻方,原幻方如下:
| 1 | 15 | 14 | 4 |
| 12 | 6 | 7 | 9 |
| 8 | 10 | 11 | 15 |
| 13 | 3 | 2 | 16 |
然后想象有一个4×4的小键盘,上面有1~16,现在同样把小键盘的对应位置上写上每一个数是第几个输入的,仍然得到一个幻方:…
埃舍尔的数学艺术
20世纪的伟大艺术家埃舍尔(Escher)是个与众不同的画家,是个和我差不多的数学Geek。他的所有艺术品都不是通常的画作,而是充满数学气息或者是现实中不可能的视觉错觉作品。在所有艺术家中,我最欣赏的就是埃舍尔,甚至甚于达芬奇。虽然埃舍尔的作品初期被当作异类来排斥,但是随着岁月流逝,越来越多的人狂热的喜爱起了他的作品,尤其是对数学有癖好的人。这篇文章将带着大家看看埃舍尔是如何将数学与艺术完美结合。
给大家展示的第一幅画叫《天使与魔鬼》,是我见过的最强的艺术品。这不是一个普通的圆,而是一个非欧几何空间,最早是由庞加莱(Poincaré)(又被翻译成彭加勒)提出了这个模型(参看我的这篇文章)。而填充整个非欧几何空间的,居然是有着强烈反差的白色天使和黑色魔鬼,真是绝了!
 …
…
圆的弦比内接正三角形之边大的概率是多少?
 圆的弦比内接正三角形之边大的概率是多少?
圆的弦比内接正三角形之边大的概率是多少?
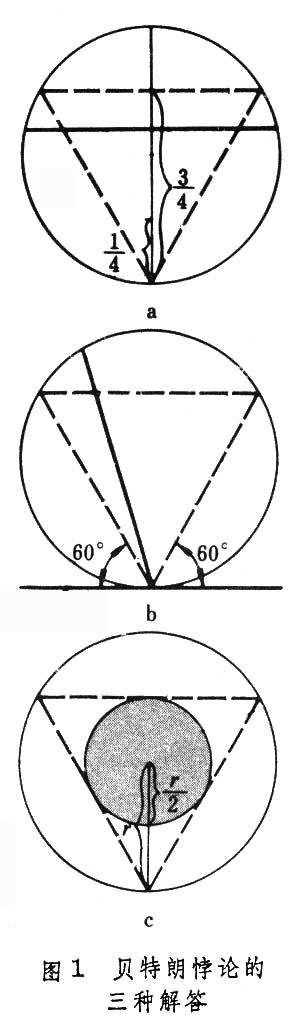
偶然间从庞加莱(Poincaré)(又被翻译成彭加勒)的《科学与假设》的概率演算这一章看到了这个命题,他最早由贝特朗提出,故又叫做贝特朗悖论。这一问题有三种解答,答案分别是1/2、1/3和1/4,我怎么也想不清楚到底哪一种是对的,其他的为什么错了,请路过的大牛们帮忙看一看。
解法一:由于对称性,可预先指定弦的方向。作垂直于此方向的直径,只有交直径于1/4 点与 3/4 点间的弦,其长才大于内接正三角形边长。所有交点是等可能的,则所求概率为1/2 。
解法二:由于对称性,可预先固定弦的一端。仅当弦与过此端点的切线的交角在60°~ 120° 之间,其长才合乎要求。所有方向是等可能的,则所求概率为1/3 。
解法三:弦被其中点位置唯一确定。只有当弦的中点落在半径缩小了一半的同心圆内,其长才合乎要求。中点位置都是等可能的,则所求概率为1/4。
这个问题的答案到底应该是多少呢?
顺便说一下,《科学与假设》里有一个观点我很认同,他觉得古典概型中概率的定义不严谨。定义:“若只有有限个不同的基本事件,且每个基本事件发生的可能性是均等的,则事件A的概率等于事件A包含的基本事件数除以基本事件总数。”可是,定义中出现的“可能性是均等的”如何判断?这是不是用概率来定义概率了?这样的定义不算循环定义么?
注:文中的三种解法及图片来自百度百科。…
棋盘覆盖问题
有一个经典问题:8*8的棋盘,去掉了左下角和右上角2个格子,请问能否用31块1*2的骨牌覆盖整个棋盘。这个问题的答案应该人人都知道吧,染色之后一目了然。
那么,有人要问了:如果去掉的是1红1白的格子各一个,结果是怎样的呢?比如下面的这个图:
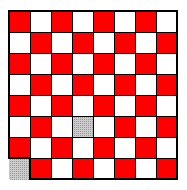
你可以自己画几个图试一试。你能证明一定可以覆盖?还是可以给出反例呢?…
两个好玩的数学游戏
这两个数学游戏,为佘飞所发明,个人认为相当有意思,我们玩儿了好长时间了,作为无聊繁重的课业之余的休闲娱乐活动。
1. 两人轮流从1~20中写数字,谁写下的数字中有4个之和为40谁就是赢家。写数字的时候每一轮都是分别写好然后再同时亮出来,已经写过的数字以后不可以再重复写。如果出现某一轮两人写的数各自可以凑成和为40,则这一轮两人写下的数字被划掉,而且以后也不准再写这个数。如果某一轮两人写了同一个数字,其中甲可以用它凑出40,而乙不行,则甲的那个数就被划掉,而乙的则保留下来。如果某一轮两人写了9同一个数字而且都无法用其凑出40,则同时被保留。
下面是一次游戏作为例子:…
几道有意思的小数学题
1.“一切无理数的无理数次方一定是无理数”,试证明此命题或举出反例。
2.两人在1,2,3,……,9这九个数字中轮流取数,不准重复,谁先取到三数之和为15谁就赢了。问先走者有没有一个稳操胜券的策略?
3.汽油危机已经来临,大家都在叫油荒。分散在长长的环形公路各处的加油站所存的油量仅仅够你跑一圈而无点滴富余。请证明,如果你在一个合适的加油站开始启程,把空油箱加足了汽油,你有充分把握可以跑完一圈,不会中途抛锚。
请先仔细思考再看解答.
…


