点猜想
首先在平面上任意给定不全共线N个点，然后在点之间连线，以保证任意两个点之间都有直线连接。所谓点猜想就是说，在这样的情况下，总存在直线仅过两个点。
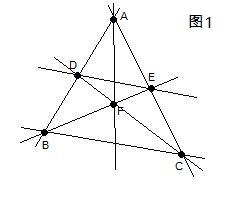如果给定了A~F六个点的位置如图，则整个图形形状就是左图，DE和AF就仅过两个点。你可以简单尝试一下，试着自己画几个点，你会发现确实无论如何也不能让所有的直线都通过三个或三个以上的点。
这个问题是小时候就见过的，在苦苦思索了好一阵子无果之后就给渐渐淡忘了。今天去图书馆看书偶然间又看到这个问题了，觉得还是挺有意思的，不过还是没什么思路。上面的介绍居然说，点猜想在被提出之后几十年内没有人能够证明！看似如此简单的问题居然还难倒了一大批人呢！但是，当最终证明被发现时，虽然思路非常灵活巧妙，却是异乎寻常的简单，连初中生都能看懂！不知你能不能自己证出这个猜想呢？…
关于e、Pi和整数之间关系的重大发现
今天我偶然的发现了这样一个令人吃惊的事实：数学中最重要的两个无理数e和Pi居然和整数有一个绝妙的联系，请看下式：
$$e^{\sqrt{163}\pi}=262537412640768744$$
等式的右边居然是一个整数！
当然这个等式用中学统一发的小计算器是验证不了的，因为显示位数不够；Windows自带的那个傻乎乎的计算器貌似也不行，除非你给出足够精确的Pi的值。如果你安装了Mathematica的话可以进行简单的验证，比如N[E^(Sqrt[163]*Pi), 20]或者N[E^(Sqrt[163]*Pi), 25]等等，可以验证这样一个惊人的等式。…
趣题：求两圆柱相交部分的体积
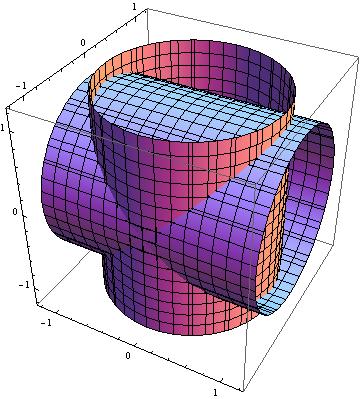
昨天去图书馆看趣味数学大师马丁加德纳的小册子《意料之外的绞刑》，看到了这个趣题：求两圆柱相交部分的体积（两圆柱半径都为1）（正交）。要求是不用微积分，只用高中生就能看懂的简单数学。如果你难以想象那部分到底是个什么形状，下面这幅图可以帮帮你。
…
3.14 Today Is Pi Day!
又是好久没有写什么东西了 哎 越是在家闲着就越懒 今天是传说中的白色情人节 不过这跟我没什么关系 今天还是Pi Day 那就说说Pi吧 顺便再熟练一下Tex
首先写一些有关$$\pi$$的漂亮的表达式。第一个表达式是最常见的一个，也就是这个表达式曾经激起了我无尽的好奇心，引我走上了自学微积分的道路。其证明在这篇文章中有。
$$\frac{\pi}{4}=1-\frac{1}{3}+\frac{1}{5}-\frac{1}{7}+\frac{1}{9}-\frac{1}{11}+…$$
$$\frac{\pi^2}{6}=\frac{1}{1^2} + \frac{1}{2^2} + \frac{1}{3^2} + \frac{1}{4^2} + \cdots $$…
貌似违背理性人假设的一组选择
最近正在看《牛奶可乐经济学2》，有一个原理下面的例子挺神奇的，我想看看是不是像他说的那样，因此发起了这个投票。请大家略加思考以后如实作答，在AB里面选择一项，CD里面选择一项，EF里面选择一项，谢谢配合！对此次投票的解释我将过几天再写。
[poll=2]Update on 2009.2.28:…
庞加莱的几何学
最近在看庞加莱（Poincaré）（又被翻译成彭加勒）的《科学与假设》，这是一本闪耀着思想光辉的圣书。介绍科学知识的书很多很多，但是像《科学与假设》这种写科学哲学的书恐怕很难找得到。虽然这本书的语言非常艰涩难懂，但这本书我至少读过3遍，每一遍都能读出一些新的感悟。
在这本书里，庞加莱对几何学提出了几条思想很深刻的见解：
1.几何学公理既非综合判断，也非实验经验，他们是约定。约定是心智的产物，约定的选择是自由的，但又不是随意的。
2.假使自然界没有固体，便不会有几何学。欧几里德几何学的性质与天然固体非常符合。
3.欧几里德几何学不比非欧几何学更真，他只是更为方便而已。经验在任何时候都不会与欧几里德共设相矛盾，同样任何经验永远也不会和罗巴切夫斯基共设相矛盾。
4.可以建立一本词典，把非欧几何的术语和欧几里德几何的术语之间建立一一对应的关系，这样非欧几何将永远不会和欧几里德几何相矛盾。
5.实验告诉我们的是物体之间的相互关系；至于物体与空间的关系，或者空间个部分的互相关系，没有一个实验影响或者能够影响。实验与空间无关，而与物体有关。
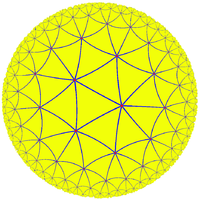
为了对非欧几何加以诠释，庞加莱在这本书里提到了著名的庞加莱圆盘模型，这个模型是非常有意思的：
…
