辛普森悖论:诡异的男女比例
大学的男女比例问题一直是广大宅男同胞所关心的重大问题,也是高中同学聚会时必然谈起的话题,对于选择大学来说,这也是一项重要指标~..
一天,我拿出两个大学(P大和T大)的统计数据开始研究。“物理学院,P大男女比例大于T大;数学科学学院,P大男女比例又是大于T大…哇,怎么所有专业P大的男女比例都高于T大啊…那还犹豫什么呢,我肯定报T大了!”正当我刚刚心意已定的时候,突然看到了统计数据的最后一行:P大的总体男女比例低于T大!“什么?!有没有搞错?怎么可能P大的所有专业男女比例都高于T大,但是整体男女比例却低于T大了呢?!肯定是哪里算错了吧…”于是我拿出计算器狂敲,却发现没有任何一个计算错了的数据,这种情况真的可能发生吗?
多说无益,请看下面编造出来的一份男女比例数据:(其中假设两所大学都只有物院和外院两个专业)
物院的数据:
| 男生人数 | 女生人数 | 男:女 | |
| P大 | 45 | 8 | 5.6:1(大) |
| T大 | 101 | 51 | 2.0:1 |
外院的数据:
| 男生人数 | 女生人数 | 男:女 | |
| P大 | 50 | 201 | 0.25:1(大) |
| T大 | 9 | 92 | 0.10:1 |
学校整体数据(即上述两个专业人数之和):
| 男生人数 | 女生人数 | 男:女 | |
| P大 | 95 | 209 | 0.45:1 |
| T大 | 110 | 143 | 0.77:1(大!) |
数据可不会是骗人的,不信可以自己动手验算一下,真的出现了这种违背常理的情况!这种现象被称为“辛普森悖论”,虽然这么叫,但其实这不是个真正的悖论,它内部没有包含逻辑上的矛盾,只是违背了人们的常理。…
复数方法巧解平面几何题
快放假了才买到《复分析——可视化方法》这本书,相见恨晚啊,这本神书,如果我能早点读,这学期的复变函数估计就学的不会这么吃力了。。。在这本书开头的地方有一个用复数方法解决平面几何问题的例子,我一看便惊了:这正是我初中时候见到的一道印象极其深刻的平面几何题,曾为它绞尽脑汁也没有想出做法呢,然而这本书就用复数的方法巧妙而自然给解决了~ 贴出来共享一下。
题是这样的:证明,在任意四边形的四条边上各做一个正方形,那么连接相对的正方形中心的线段互相垂直并且等长。示意图如下。
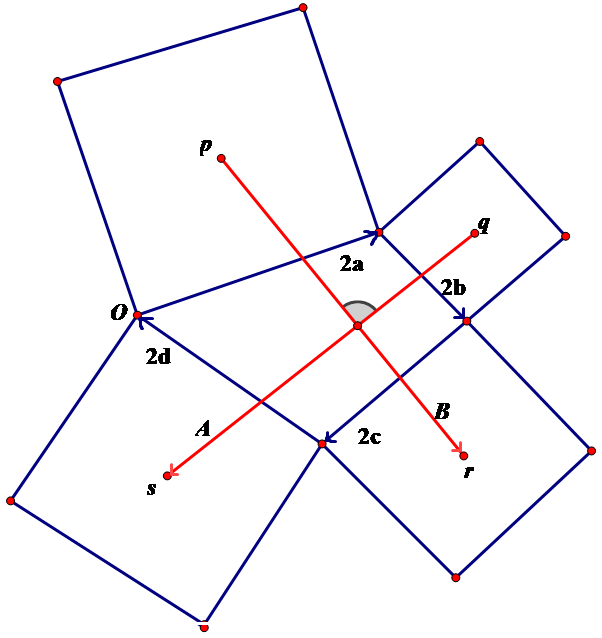 …
…
椭圆颂
/*突然想起来有这么篇文章的存在 不想让它被遗忘在互联网最边缘的阴暗角落 于是就当一下勤劳的搬运工吧..此诗作者是三国杀界著名的蒙太奇..*/
椭圆颂
点猜想
首先在平面上任意给定不全共线N个点,然后在点之间连线,以保证任意两个点之间都有直线连接。所谓点猜想就是说,在这样的情况下,总存在直线仅过两个点。
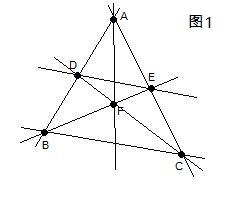 如果给定了A~F六个点的位置如图,则整个图形形状就是左图,DE和AF就仅过两个点。你可以简单尝试一下,试着自己画几个点,你会发现确实无论如何也不能让所有的直线都通过三个或三个以上的点。
如果给定了A~F六个点的位置如图,则整个图形形状就是左图,DE和AF就仅过两个点。你可以简单尝试一下,试着自己画几个点,你会发现确实无论如何也不能让所有的直线都通过三个或三个以上的点。
这个问题是小时候就见过的,在苦苦思索了好一阵子无果之后就给渐渐淡忘了。今天去图书馆看书偶然间又看到这个问题了,觉得还是挺有意思的,不过还是没什么思路。上面的介绍居然说,点猜想在被提出之后几十年内没有人能够证明!看似如此简单的问题居然还难倒了一大批人呢!但是,当最终证明被发现时,虽然思路非常灵活巧妙,却是异乎寻常的简单,连初中生都能看懂!不知你能不能自己证出这个猜想呢?…
趣题:求两圆柱相交部分的体积
昨天去图书馆看趣味数学大师马丁加德纳的小册子《意料之外的绞刑》,看到了这个趣题:求两圆柱相交部分的体积(两圆柱半径都为1)(正交)。要求是不用微积分,只用高中生就能看懂的简单数学。如果你难以想象那部分到底是个什么形状,下面这幅图可以帮帮你。
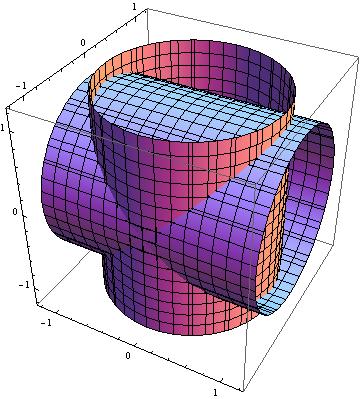 …
…
庞加莱的几何学
最近在看庞加莱(Poincaré)(又被翻译成彭加勒)的《科学与假设》,这是一本闪耀着思想光辉的圣书。介绍科学知识的书很多很多,但是像《科学与假设》这种写科学哲学的书恐怕很难找得到。虽然这本书的语言非常艰涩难懂,但这本书我至少读过3遍,每一遍都能读出一些新的感悟。
在这本书里,庞加莱对几何学提出了几条思想很深刻的见解:
1.几何学公理既非综合判断,也非实验经验,他们是约定。约定是心智的产物,约定的选择是自由的,但又不是随意的。
2.假使自然界没有固体,便不会有几何学。欧几里德几何学的性质与天然固体非常符合。
3.欧几里德几何学不比非欧几何学更真,他只是更为方便而已。经验在任何时候都不会与欧几里德共设相矛盾,同样任何经验永远也不会和罗巴切夫斯基共设相矛盾。
4.可以建立一本词典,把非欧几何的术语和欧几里德几何的术语之间建立一一对应的关系,这样非欧几何将永远不会和欧几里德几何相矛盾。
5.实验告诉我们的是物体之间的相互关系;至于物体与空间的关系,或者空间个部分的互相关系,没有一个实验影响或者能够影响。实验与空间无关,而与物体有关。
为了对非欧几何加以诠释,庞加莱在这本书里提到了著名的庞加莱圆盘模型,这个模型是非常有意思的:
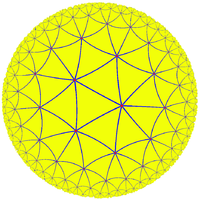 …
…


