最小作用量原理与物理之美2——费马原理
对于几何光学中的许许多多的定律,费马找到了一种统一的描述,现在被称为费马原理,被认为是最小作用量原理在几何光学中的特例,是最小作用量原理最早的成功例子。上一篇文章并没有真正写最小作用量原理,写的仅仅是一些简单的极值问题(千万不要认为那就是最小作用量原理),而本文与下一篇文章则将写最小作用量原理在几何光学与动力学的特例,并给出比较精确的数学公式(这是为了后面的横向比较和更深刻地理解最小作用量原理),对微积分头痛的人可以跳过公式只看文字。
费马原理是这么说的:过空间中两定点的光,实际路径总是光程最短、最长或恒定值的路径。
其中光程定义为该介质的折射率乘以路程。写成数学的形式就是:
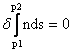
其中,δ是变分符号,p1、p2表示空间中两个固定点,n为介质的折射率,s表示路程。为了理解上式的含义,我们需要和导数做一个类比。我们对一个函数求导数,如果导数值等于零,那么可以判断出原函数在该点处会取得极小值、极大值或恒定值。上面的式子和导数有一个显著的不同,导数研究的是以字母为自变量的函数的极值,而上式想求的则是以一个函数(位置随时间变化的函数)为自变量的泛函的极值。我们把每一条路径看作是位置随时间变化的函数,把这个函数看作自变量,我们要求的则是各条路径中光程取极值的那条路径;就像我们求导求的是各个x中使得y取极值的那个点。函数求极值可以用导数,泛函求极值则可以用变分法,即δS=0(其中S是一个泛函)。大家就把δ理解成和导数相类似的东西就可以了。…
拓扑学与克莱因瓶
前几天借了图书馆的一本《拓扑实验》闲着没事儿看,结果令我惊奇的是我周围的大牛们居然没有几个人听说过拓扑学。这么有意思的一个数学分支,不知道的话也太可惜了。
拓扑学是一门新兴的学科,大概是从20世纪开始正式被人们所研究的。它和以往人们所研究的几何不同,以前人们关注的东西是几何图形或几何体的角度、长度、面积、体积等,而拓扑学则研究的则是经过一系列扭曲、拉伸、压缩等操作仍然不变的性质。比如说,一个篮球可以被我拉成一个橄榄球,尽管形状变了,可能体积、表面积都变了,但是有一些重要性质是没有变化的:有两个面(内表面和外表面),封闭等。这些都是拓扑学的性质,这些都属于拓扑学的范畴。大家都很熟悉莫比乌斯带吧,它也是拓扑学的典型研究对象。
回到正题上。今天我想说的是拓扑学中的克莱因瓶。这是一种奇怪的瓶子,他有这么几个重要的性质:只有一个面,没有棱,没有顶点。这么个东西是很难凭空想象的,所以下面放了几张图可以供大家想象。…
一道难题巧解
这道题来自孙丕业在福州上的课。当时老师出了这道题,等了半个小时无人能给出完整的解答,大家都讨论的焦头烂额却也没什么结果。这时,老师开始讲题了,只一句话,大家就全明白了,接着全体鼓掌!当时孙丕业给我看这道题,我也想了半天没有任何思路,结果他又是一句话把我搞懂!
这道题是这样的。n为奇数,用n-3条不交叉的直线可以把正n边形分成n-2个三角形,求证:有且仅有一个三角形是锐角三角形。
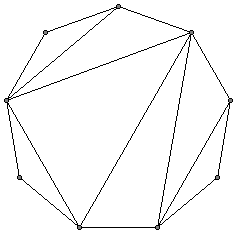
请先认真思考再看下面的解答。…
一个小发现
那天和同学一起讨论时,发现了一个很有意思的东西:
圆的周长公式:C=2*π*R
圆的面积公式:S=π*R^2
这两个公式间,有一个巧妙的联系:对面积公式进行求导即得到周长公式,即dS/dR=C.
球的表面积公式:S=4*π*R^2
球的体积公式:V=4/3*π*R^3
这两个公式间,同样也存在着类似的关系:对体积公式求导即得到表面积公式,即dV/dR=S!!!
我觉得挺有意思的,就上网查了一下有关4维的情形:
“超球”(4维球)的“表体积”公式:V=2*π^2*R^3
“超球”的“超体积”公式:W=1/2*π^2*R^4
(这组公式从网上查的,可能并不很权威,欢迎指出错误之处)
/*update:当时不太明白,现在学了积分了,就一目了然了。就是一圈一圈积分。*/…
有趣的测试你反应能力的一套题
你想测试一下你的反应速度是灵敏还是迟钝么?你想看一看你的聪明程度是否很高么?那么,就请做一下下面这一套提吧,题目很简单,记住,一定要按照顺序作,否则就别做。最后一道题是最考验人的一道题,呵呵,要大约估计一下做这道题的时间。请再作出一道题之前不要看答案,否则没有效果。
1.把这个图形分成全等的两份。…
奇妙的证明:周长相等的所有平面图形中,圆的面积最大
我首先要证明,面积最大的图形满足一个性质:一条平分周长的直线(暂且把它叫做周长平分线),一定也平分面积。因为,如果不平分面积的话,那么我总可以把面积较大的那块翻到另一边去,使得周长不变,而面积增大(如左图,红色曲线围成的面积大于蓝色曲线)。好了,接下来,我要再证明面积最大的图形满足第二条性质:周长平分线与曲线的两个交点和曲线上任意一点构成的三角形,必然是直角三角形。因为,如果它不是直角三角形,我可以把他拉伸或压缩一下,使它成为直角三角形,这样新三角形的面积大于原三角形的面积(证明省略,主要使用S=absinθ/2),而图形其他部分面积不变,这样面积就扩大了。因此,面积最大的图形满足上述两条性质,我们就不难推出它是圆了。
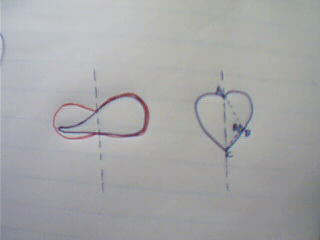 …
…


