盘点数学里十大不需要语言的证明
0. 勾股定理&余弦定理
这个大家小学就学过的古老定理,有着无数传奇故事。我可以很随意的写出她的10个不同的证明方法。而路明思(Elisha Scott Loomis)在 《毕达哥拉斯命题》( Pythagorean Proposition)提到这个定理的证明方式居然有367种之多,实在让人惊讶。这里给出一个不需要语言的证明方法。

实际上勾股定理是余弦定理的一种特殊情况,而余弦定理的证明,同样可以不用语言。
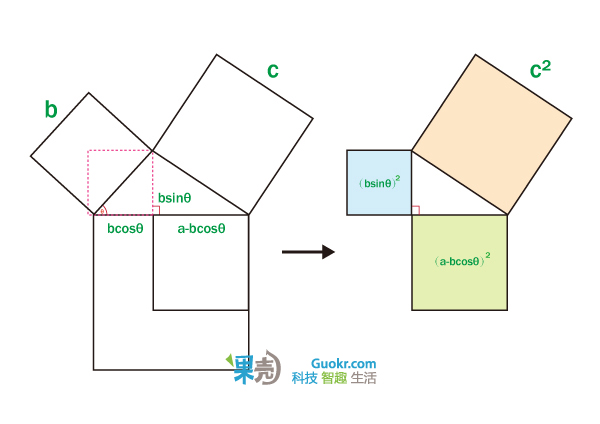
1. 关于反正切的恒等式
…辛普森悖论:诡异的男女比例
大学的男女比例问题一直是广大宅男同胞所关心的重大问题,也是高中同学聚会时必然谈起的话题,对于选择大学来说,这也是一项重要指标~..
一天,我拿出两个大学(P大和T大)的统计数据开始研究。“物理学院,P大男女比例大于T大;数学科学学院,P大男女比例又是大于T大…哇,怎么所有专业P大的男女比例都高于T大啊…那还犹豫什么呢,我肯定报T大了!”正当我刚刚心意已定的时候,突然看到了统计数据的最后一行:P大的总体男女比例低于T大!“什么?!有没有搞错?怎么可能P大的所有专业男女比例都高于T大,但是整体男女比例却低于T大了呢?!肯定是哪里算错了吧…”于是我拿出计算器狂敲,却发现没有任何一个计算错了的数据,这种情况真的可能发生吗?
多说无益,请看下面编造出来的一份男女比例数据:(其中假设两所大学都只有物院和外院两个专业)
物院的数据:
| 男生人数 | 女生人数 | 男:女 | |
| P大 | 45 | 8 | 5.6:1(大) |
| T大 | 101 | 51 | 2.0:1 |
外院的数据:
| 男生人数 | 女生人数 | 男:女 | |
| P大 | 50 | 201 | 0.25:1(大) |
| T大 | 9 | 92 | 0.10:1 |
学校整体数据(即上述两个专业人数之和):
| 男生人数 | 女生人数 | 男:女 | |
| P大 | 95 | 209 | 0.45:1 |
| T大 | 110 | 143 | 0.77:1(大!) |
数据可不会是骗人的,不信可以自己动手验算一下,真的出现了这种违背常理的情况!这种现象被称为“辛普森悖论”,虽然这么叫,但其实这不是个真正的悖论,它内部没有包含逻辑上的矛盾,只是违背了人们的常理。…
有趣的颜色错觉
1.这张是最著名也最牛逼的颜色错觉图。你认为A和B所在的方格颜色相同吗?你必然不相信,但是如果捂住图的其他部分,只露出这两个块,就大体会相信了;然后你可以用Photoshop或者画图取色验证一下,会发现,两个方块的颜色确确实实是完全相同的!

2.现在你还敢说,下图两个灰色区域颜色深浅不同吗?自己按照上图方法验证一下便可知晓真相..…
趣题:求两圆柱相交部分的体积
昨天去图书馆看趣味数学大师马丁加德纳的小册子《意料之外的绞刑》,看到了这个趣题:求两圆柱相交部分的体积(两圆柱半径都为1)(正交)。要求是不用微积分,只用高中生就能看懂的简单数学。如果你难以想象那部分到底是个什么形状,下面这幅图可以帮帮你。
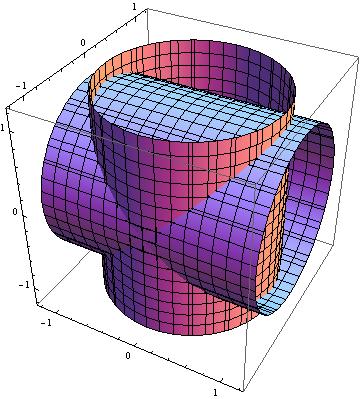 …
…
埃舍尔的数学艺术
20世纪的伟大艺术家埃舍尔(Escher)是个与众不同的画家,是个和我差不多的数学Geek。他的所有艺术品都不是通常的画作,而是充满数学气息或者是现实中不可能的视觉错觉作品。在所有艺术家中,我最欣赏的就是埃舍尔,甚至甚于达芬奇。虽然埃舍尔的作品初期被当作异类来排斥,但是随着岁月流逝,越来越多的人狂热的喜爱起了他的作品,尤其是对数学有癖好的人。这篇文章将带着大家看看埃舍尔是如何将数学与艺术完美结合。
给大家展示的第一幅画叫《天使与魔鬼》,是我见过的最强的艺术品。这不是一个普通的圆,而是一个非欧几何空间,最早是由庞加莱(Poincaré)(又被翻译成彭加勒)提出了这个模型(参看我的这篇文章)。而填充整个非欧几何空间的,居然是有着强烈反差的白色天使和黑色魔鬼,真是绝了!
 …
…

 …
…
