最小作用量原理与物理之美3——牛顿力学

就像最小作用量原理可以推导出所有几何光学定律一样，力学中也存在一个最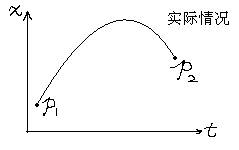小作用量原理的特例可以推导出整个牛顿力学。今天我们就来研究研究这个。

有这样一个事实：假定有一个质点在引力场中通过自由运动从某处移动至另一处——你把它抛出去，他就会上升又落下。如果画出x-t图（为了简化，只考虑一维的运动，设x轴是竖直的轴），那么运动图像是一条抛物线。你可以尝试着通过起点和终点画一些别的曲线，如果计算出经历整条路径期间动能减重力势能对时间的积分，你会发现所获得的数值比实际运动所获得的要大。如果我们设作用量S为

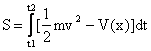
那么上面的事实换句话说就是作用量S在实际运动中取得最小值。对上面字母的解释：t1、t2表示运动的起点和终点时刻，1/2*m*v^2是研究物体的动能，V(x)是其势能（这里把它写成是随x变化的函数）。当物体只受重力的时候，V(x)=mgx。我们在上一篇文章中说过，一个泛函取得极值可以令其变分等于0，所以在力学中，最小作用量原理的特例就写作：…

最小作用量原理与物理之美2——费马原理

对于几何光学中的许许多多的定律，费马找到了一种统一的描述，现在被称为费马原理，被认为是最小作用量原理在几何光学中的特例，是最小作用量原理最早的成功例子。上一篇文章并没有真正写最小作用量原理，写的仅仅是一些简单的极值问题（千万不要认为那就是最小作用量原理），而本文与下一篇文章则将写最小作用量原理在几何光学与动力学的特例，并给出比较精确的数学公式（这是为了后面的横向比较和更深刻地理解最小作用量原理），对微积分头痛的人可以跳过公式只看文字。

费马原理是这么说的：过空间中两定点的光，实际路径总是光程最短、最长或恒定值的路径。
其中光程定义为该介质的折射率乘以路程。写成数学的形式就是：

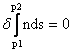
其中，δ是变分符号，p1、p2表示空间中两个固定点，n为介质的折射率，s表示路程。为了理解上式的含义，我们需要和导数做一个类比。我们对一个函数求导数，如果导数值等于零，那么可以判断出原函数在该点处会取得极小值、极大值或恒定值。上面的式子和导数有一个显著的不同，导数研究的是以字母为自变量的函数的极值，而上式想求的则是以一个函数（位置随时间变化的函数）为自变量的泛函的极值。我们把每一条路径看作是位置随时间变化的函数，把这个函数看作自变量，我们要求的则是各条路径中光程取极值的那条路径；就像我们求导求的是各个x中使得y取极值的那个点。函数求极值可以用导数，泛函求极值则可以用变分法，即δS=0（其中S是一个泛函）。大家就把δ理解成和导数相类似的东西就可以了。…

最小作用量原理与物理之美1——自然中无处不在的极值

观察自然界的各种现象，会发现极值往往出现。知道这一点非常重要，在最小作用量被明确提出之前，人们已经研究了很多极值问题。我们先来看一些比较简单的极值问题，会对最小作用量原理有一个更深刻的认识，也能从中看出最小作用量原理的起源与历史。

物理定律都有两种表述形式：一种是普通的我们高中学的形式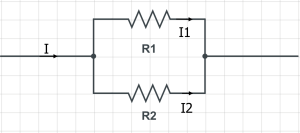，用力、加速度、电场强度等概念描述的物理定律；另一种是极值的形式，在一个物理过程中某个量取得极值。这两种表述形式是等价的。

先看一个最简单的例子，如图，两个电阻R1、R2并联，输入的电流为I，求I1、I2是多少。
这个问题初中生都会做，用并联时电压相等加上欧姆定律就可以作了。可以容易的求得

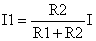
现在我们换一种方法：I1、I2的取值使得热功率最小。…