24
Aug
一个超级赖皮的数学证明方法——例证法
今天看到《数学家的眼光》（张景中著）写到了一个巨赖皮的数学证明方法，叫例证法，看完我都惊得不行了，就写到这里来和大家分享一下。
为了说明例证法，我们举一个简单的例子。试证明：(x+1)(x-1)=x^2-1。我们假设我们不会做（这不是在贬低你的智商阿）。现在我就讲一个所有人都肯定能学会的方法，用例证法来证明！
证明：令x=1代入原式，发现等式成立。
令x=2代入原式，发现等式成立。
令x=3代入原式，发现等式成立。
所以原式恒成立。
你看了可能会狂笑不止，有种想揍我的冲动，这什么东西，举了3个例子就说证明了原式？证明等式成立可必须是所有x都满足才行啊！可是，且慢，我可以告诉你，这样证明是严谨的。不信就听我仔细分析。…
3
Jun
一张图证明著名等式
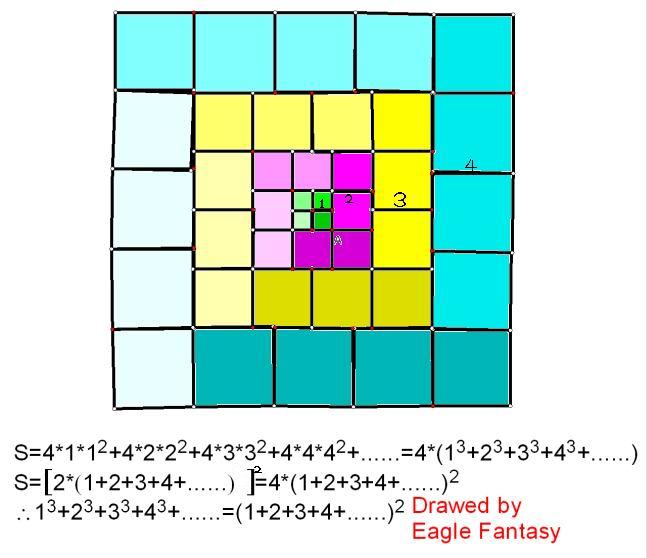
如图，从内到外各圈正方形的边长依次是1，2，3，4……通过面积的两种表达形式，就可以证明结论中的著名等式！
解释一下：第一个算式是把面积一圈一圈加起来，第二个是总边长的平方。…
18
May
证明：三角形的质心是三条中线交点
这个命题肯定是成立的，没有人敢怀疑。但是，我就想不明白为什么会是这样。并不是画一条线，只要把面积平分了，质心就一定在这条线上。因为把它吊起来，两边虽然重力相同，可力臂未必相同。
我曾尝试过多种证法。比如定义法，根本无从研究；负质量法，完全无法下手；积分法，太繁琐而且变数太多不好操作；巴普斯定理，也显得不能胜任……怎么办？
我问了我们学校最牛的物理竞赛教练王林老师，他考虑了一会，先做了几次失败的尝试，后来突然恍然大悟，想到了一个绝妙的好方法！…
