赌场是凭借这个方法赚钱的吗？

众所周知，去赌场赌博，赢钱的一定是庄家。通过概率的不均等让你赔钱你肯定陪得心服口服，但是有人提出了这样一种赌场赚钱的方法，即使是输赢概率为1/2赌场也会赚钱，乍看起来似乎确实有道理：

就假设赌徒跟赌场玩的是赌大小的问题，输赢概率是严格的1/2。赌徒身上带着5元钱，每次下注1元。如果赌徒身上的钱在某个时刻输光了，那么赌徒就会离开赌场回家；如果赌徒连续赌了1000次都没有输光，赌徒在这个时刻就会停止赌博结算完毕回家去。如此一来，利用赌徒停止赌博两个边界条件的不对称性，随着赌徒增多，赌场就可以从中赚钱了~！

乍看似乎确实有道理，因为不仔细想的话会觉得赌徒输钱离开赌场的概率似乎确实比较大。但是如果写一个程序跑一跑看看赌场最终会赚多少钱，结果会出乎意料：赌场赚到的钱数将会在基本上以0为中心的一个范围内震荡，并不会随着赌徒人数增多而增多！

问题出在哪呢？其实这个结果也不算过于出乎意料。因为虽然赌徒输钱离开的概率是比较大的，但是他赔的钱就那么些；但是赌徒如果是赌了1000次才离开的，走的时候赚走的钱数可能相比而言是很多的。于是二者的作用是有可能恰好抵消的。如果你有耐心做详细的定量数学计算的话，其实是可以解析的给出这个问题的结果的，赌场赚到的钱数随赌徒人数怎么变化是可以精确算出来的。

但是还有一种很巧妙地思路可以一下子看出来，其实赌场从期望上来说就是不赚的！仔细想一下：…

由哥白尼原理推导人类文明灭亡时间

/*这篇文章的主要内容由热学欧阳颀老师所讲 出自某期New York Times*/

下面要进行的一段推导，将十分诡异，可能有点莫名其妙的感觉，不过还是请完整看下去~
首先说一下什么是哥白尼原理。

Copernican principle:
The best theories are those that do not require the observer to live in a special place in the universe or at a special time in history in order to be true.

一个与直觉相悖的概率问题及其引发的严肃思考

一人用颤抖的双手拿着艾滋病检测呈阳性的化验单去找医生：

“医生，弱弱的问一句，这个检测呈阳性是什么意思啊？”

医生：“同志，做好心理准备，你很有可能要悲剧了…目前艾滋病在世界上比较严重，粗略估计大概每1000人中就有一人得艾滋病。我们采用的是某种血液试验检测法用于检测身体中是否含有艾滋病病毒，这种方法相当精确，但也可能带来两种误诊。首先，他可能会让某些真有艾滋病的人得到阴性结果，称为假阴性，不过只有0.05的概率发生；其次，它还可能让某些没有艾滋病的人得到阳性结果，称为假阳性，不过只有0.01的概率会发生。根据这些数据，你差不多可以估计出来自己的囧况了…”

那人：“我X，哥悲剧了…”

OK虚拟的情境到此打住，我现在要问一个问题，请先不要计算，先尝试着用直觉给出一个答案：如果你就是这位哥，在艾滋病检检测呈阳性的条件下，你真的得了艾滋病的概率是多大呢？

请从下面ABC三个选项中选出与你的直觉最接近的：A.90%;  B.50%;  C.10%。…

猫捉老鼠问题

这个是我室友的力学老师留给他们的思考题，因为它完全符合思维过程相当困难、但是解答却极为漂亮简单的原则，所以我就转过来分享一下。

在数轴上，0的位置停着一个不动的老鼠，1的位置在初始时刻有一只猫。猫是可以走动的，每一步在数轴上分别以二分之一的概率或朝着正方向或朝着负方向走1的距离。当猫到达0的位置时，猫就抓到老鼠了，游戏结束。问当猫走的步数趋向于无穷大的时候，最终捉到老鼠的概率是多大？一定要先仔细思考再看解答……

有趣的无规行走模型

昨天和一帮子同学出去玩，晚饭时间点完菜等待上菜的时候有两个同学玩起了一个非常无聊的游戏：甲同学扔硬币，乙同学猜正反面，如果乙猜对了则乙的鼻子变长1cm，反之如果乙猜错了则鼻子缩短1cm。（这个是和谐过的版本，原始版本变长变短的不是鼻子而是另一个猥琐的东西…）。他们正在无聊的玩，全然不知道这么玩下去他鼻子长度的绝对值期望是多少…其实，这正是我高一的时候在费恩曼物理学讲义上看到的一个数学模型：Random Walk（无规行走）。对于这个模型，我敢说绝大多数人凭直觉会觉得鼻子长度的绝对值最终的期望值会是0，但事实绝非如此，你可以自己扔几次硬币试试，正确的答案应该是你扔硬币次数N的平方根！

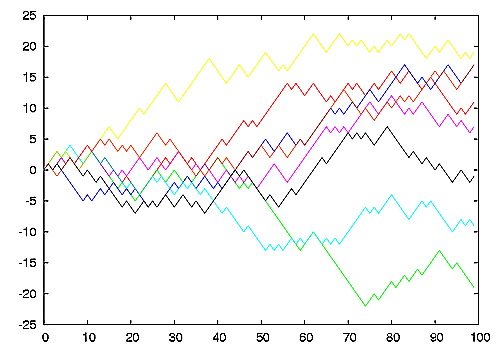
下面给出证明，该证明基本来自《费恩曼物理学讲义》第一卷：…

圆的弦比内接正三角形之边大的概率是多少？

圆的弦比内接正三角形之边大的概率是多少？

偶然间从庞加莱（Poincaré）（又被翻译成彭加勒）的《科学与假设》的概率演算这一章看到了这个命题，他最早由贝特朗提出，故又叫做贝特朗悖论。这一问题有三种解答，答案分别是1/2、1/3和1/4，我怎么也想不清楚到底哪一种是对的，其他的为什么错了，请路过的大牛们帮忙看一看。

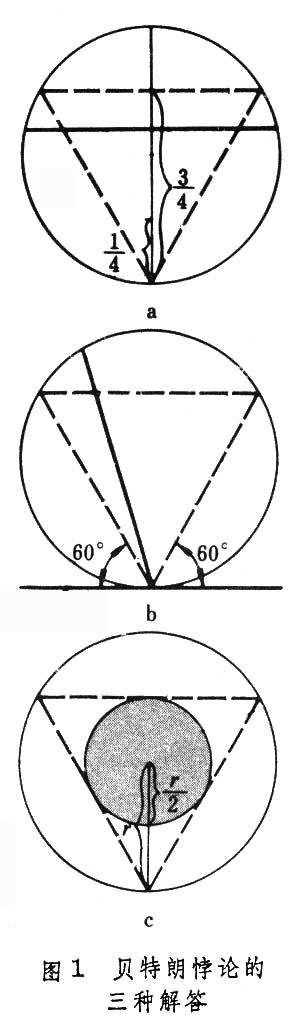
解法一：由于对称性，可预先指定弦的方向。作垂直于此方向的直径，只有交直径于1/4 点与 3/4 点间的弦，其长才大于内接正三角形边长。所有交点是等可能的,则所求概率为1/2 。

解法二：由于对称性，可预先固定弦的一端。仅当弦与过此端点的切线的交角在60°～ 120° 之间，其长才合乎要求。所有方向是等可能的，则所求概率为1/3 。

解法三：弦被其中点位置唯一确定。只有当弦的中点落在半径缩小了一半的同心圆内，其长才合乎要求。中点位置都是等可能的,则所求概率为1/4。

这个问题的答案到底应该是多少呢？

顺便说一下，《科学与假设》里有一个观点我很认同，他觉得古典概型中概率的定义不严谨。定义：“若只有有限个不同的基本事件，且每个基本事件发生的可能性是均等的，则事件A的概率等于事件A包含的基本事件数除以基本事件总数。”可是，定义中出现的“可能性是均等的”如何判断？这是不是用概率来定义概率了？这样的定义不算循环定义么？

注：文中的三种解法及图片来自百度百科。…