拓扑学与克莱因瓶
前几天借了图书馆的一本《拓扑实验》闲着没事儿看,结果令我惊奇的是我周围的大牛们居然没有几个人听说过拓扑学。这么有意思的一个数学分支,不知道的话也太可惜了。
拓扑学是一门新兴的学科,大概是从20世纪开始正式被人们所研究的。它和以往人们所研究的几何不同,以前人们关注的东西是几何图形或几何体的角度、长度、面积、体积等,而拓扑学则研究的则是经过一系列扭曲、拉伸、压缩等操作仍然不变的性质。比如说,一个篮球可以被我拉成一个橄榄球,尽管形状变了,可能体积、表面积都变了,但是有一些重要性质是没有变化的:有两个面(内表面和外表面),封闭等。这些都是拓扑学的性质,这些都属于拓扑学的范畴。大家都很熟悉莫比乌斯带吧,它也是拓扑学的典型研究对象。
回到正题上。今天我想说的是拓扑学中的克莱因瓶。这是一种奇怪的瓶子,他有这么几个重要的性质:只有一个面,没有棱,没有顶点。这么个东西是很难凭空想象的,所以下面放了几张图可以供大家想象。
克莱因瓶只有一个面这一性质与莫比乌斯带很像,设想一只蚂蚁在克莱因瓶上面爬,它可以通过一定的路径走到一开始的位置的“反面”(其实没有什么反面不反面的,就一个面)。而在球皮上的蚂蚁就不打行了,他怎么爬也不可能从外表面爬到内表面去(如果这只蚂蚁太牛了,有本事到第四维空间去,那它就能做到)。
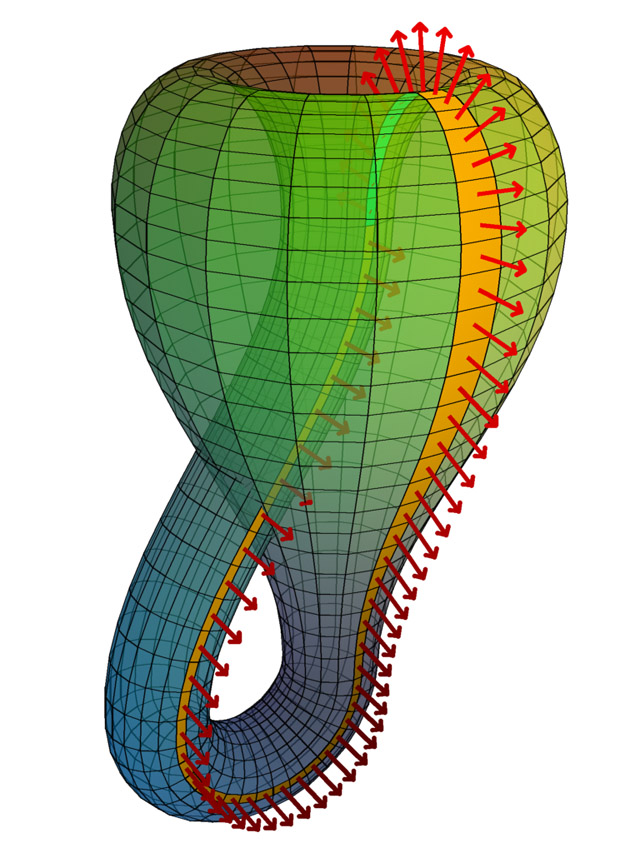
这个性质就引起了我的一个疑问。如果我用高斯定理算电通量的时候,高斯面选的是个克莱因瓶(有点儿找事儿),应该怎样规定电场线穿出的方向呢?法向量会顺着表面移动到他的反方向!(见下面那个带箭头的克莱因瓶。)
下面考考你的想象力。如果拿刀沿着对称轴竖着把克莱因瓶一劈为二,会劈出两个什么东西呢?我可以先告诉你答案,是两个莫比乌斯带,能不能想象出来就是你的事儿了,我是悟了老半天才悟出来的。
再想象点有难度的拓扑学问题。如果把莫比乌斯带那样扭半圈算是转了一下粘起来后得到的,那么有没有人能只凭想象而不做实验告诉我,把莫比乌斯带沿中间剪开得到的纸带等效于转了几下?把转了两下粘起来得到的纸带从中间剪开,肯定得到两个纸带,他们是套在一起的还是分开的,各自转了几下呢?如果有谁能想象出来这些问题,那真是神人了。





关于电通量的问题,三维情况下的公式不再适用,去看看四维情况下的公式
四维的..这就没研究过了 肯定很诡异…
。。。拓扑想象可以使用一些“技巧”。。比如适当旋转扭曲脑中的图像使其更具有对称性,然后就比较容易想象出来那个剪开之后的样子了
可克莱因瓶不是一个封闭曲面啊
克莱因瓶严格意义上只能存在于4维空间之中,那个瓶颈伸进瓶子里面的部分是从第4维伸进去的,这里展示的模型应该只能算是克莱因瓶在3维空间内的投影吧,这个模型是帮助咱们理解而已,自己想像的话太难了。
它的表面积……