physixfan

工业化之后的生育率低于世代更替率也许是个无解的问题

生育率这个话题也许对有些人来说是个显而易见的常识，但是没仔细想过这个问题的人第一次读到时可能会觉得大吃一惊，所以我还是写一写这个话题吧。

现在应该每个中国人都知道中国的生育率很低了，1.16 这个生育率确实是低到令人发指。很多人评论说自己不想生孩子的原因是住的地方太小了、生活成本太高了、生了孩子之后的教育成本太高等等。但是实际上如果看一下世界上的其他国家就会发现，虽然上面提到的这些因素的确也是降低生育率的重要原因，但是对于一个已经工业化的国家来说，即使一些发达国家已经做到了地广人稀人均大豪斯、大家都很富裕收入高物价低、公立教育免费竞争压力也不大，他们的生育率依然统统低于世代更替率的2.1。

以下列举几个不论是国民收入还是人均居住面积还是女性权益还是社会福利等各方面已经做得很不错的发达国家的数据 (source: Wikipedia)：

• United States 1.7
• United Kingdom 1.6
• France 1.8
• Germany 1.5
• Switzerland 1.5
• Canada 1.5
• Sweden 1.7
• Norway 1.5
• Finland 1.4

可见这些主要发达国家生育率都是低于2.1的。

生育率要超过2.1有多难？这可不是每对夫妻生俩娃能达到的。一个社会上总有人一辈子找不到对象、总有人想要丁克不生孩子、总有夫妻只想要1个孩子，所以需要有一部分人生3-4个或更多孩子才能抵消回去。我们假设一个国家80%的女性都生俩孩子、5%不生、5%生一个孩子，这已经是孩子很多的社会了吧，想要达到2.1的生育率，剩下10%的女性需要生多少个孩子才能把生育率拉到2.1？答案是平均要生4.5个！你每看到一个丁克女性，就要看到一个生了4胎的女性，这才能让平均值拉到2而已。即使我们不看中国，只看看美国等发达国家，生这么多娃的女性也是非常少的。

我们看看Wikipedia里的生育率数据，都有哪些国家超过了2.1？可能不用猜你也知道，基本上全是非洲国家、再加上一些伊斯兰神权国家。可以说生育率超过2.1的国家里面，我连有兴趣去旅游的国家都没有几个，想要去长期居住的国家就更加是严格为0个了。令人惊奇的是，就连大家印象里很能生的印度，生育率都已经低到2.0了。

所以这件事大概是有一定反直觉的：越是工业化的、物质生活优越的、人权得到了保障的国家，越是生的少；越是贫穷落后没人想去甚至正在战乱的国家，越是生的多。

在生育率超过了2.1的国家里面，只有一个非常特殊：Israel。这是一个标准的工业化发达国家，然而它的生育率达到了惊人的2.9。它是怎么做到的？其中一个很重要的群体是 Haredi Judaism 或者叫做 Ultra-Orthodox Judaism，这个群体实在是太特殊了：女性只管生孩子养孩子、男性只管研究圣经，别的什么都不做。不允许避孕、不允许受世俗教育、不允许你了解外面的世界。你问他们不劳作那么吃什么？政府给福利呗。就是靠着这群人，他们的女性生育率是 6.6，这才把 …

人为什么会感觉时间越过越快 以及如何“延长生命”

估计每个人对时间流逝速度的主观感觉都是：随着年纪越来越大，时间过得越来越快。对于这一现象，有两种解释都是比较靠谱的：

1. 随着年纪越来越大，每一天在生命中的占比越来越小了。一个月的时间，对于1岁的小孩来说就是生命中的1/12，而对于30岁的人来说只占1/360而已。
2. 人类的记忆功能的运作模式，会让你只记住新奇的内容，而重复的内容就不会有太多印象。当你第一次过年的时候，这个节日的每一个细节对你来说都是新的，因此你的大脑会努力记住各种内容；而当你第30次过年的时候，大脑就会偷懒，他就会默认这是众多过年中的一次，重复的内容就不去专门记了，仅仅只有少数特定细节会让你有印象了。你去回想的时候，都不一定记得起来哪个细节是哪一年的了。而随着人的年纪越来越大，人生中重复的、已经有规律的事情越来越多。每天工作的内容也都稳定可预测了，记忆点就少了很多，以至于回顾的时候会觉得好像啥都没怎么干咋一年又过去了。

这第二种解释是非常有意思的，因为第二种解释给了我们一些的启发：如何在客观上生命时间长度固定的情况下，主观上延长你的一生。这个方法就是：尽量不要让你的一天在重复中度过，要去追求新奇的体验。

追求新奇体验的最简单的方法就是旅行。和在家坐着看屏幕不同，人类在旅行时全方位沉浸在一个陌生的环境里，会让记忆深刻很多，这大概是几亿年的进化所致，想用电视剧电影模拟这种刺激是很难做到的。我自己的体会就是2020、2021这种因为新冠而不出门的日子过得飞快，每隔段时间就出去旅行的时间就会慢一些，值得回忆的时间点也多很多。

追求新奇体验的更高难度的做法是学习新知识。每天应用同样的技能，和每天都在学习新知识，时间流逝的主观体验是非常不同的。每天读书只要读的内容都是non-trivial的以前自己没想过的思考，就是一种很好的修行。更进一步的，发达国家经常看到有人年纪很大了还要换个方向读 PhD，我也有同学做腻了程序员而重新读书追求星辰大海，在我看来这都是一种能够延长主观生命的方式。

其实说穿了，一句中国的老话就能概括：读万卷书，行万里路。…

ChatGPT的画图模型DALL·E 3效果真的挺不错

终于等到我的ChatGPT账号有画图功能了，今天来把玩了一番。之前我也玩过Midjourney，但是感觉效果差强人意。而ChatGPT的DALL·E 3最令我感到惊艳的地方在于，它可以根据各种自然语言指示来对先前做出来的图进行修改。

来贴几张我画着玩的图，大家可以感受一下它的威力。

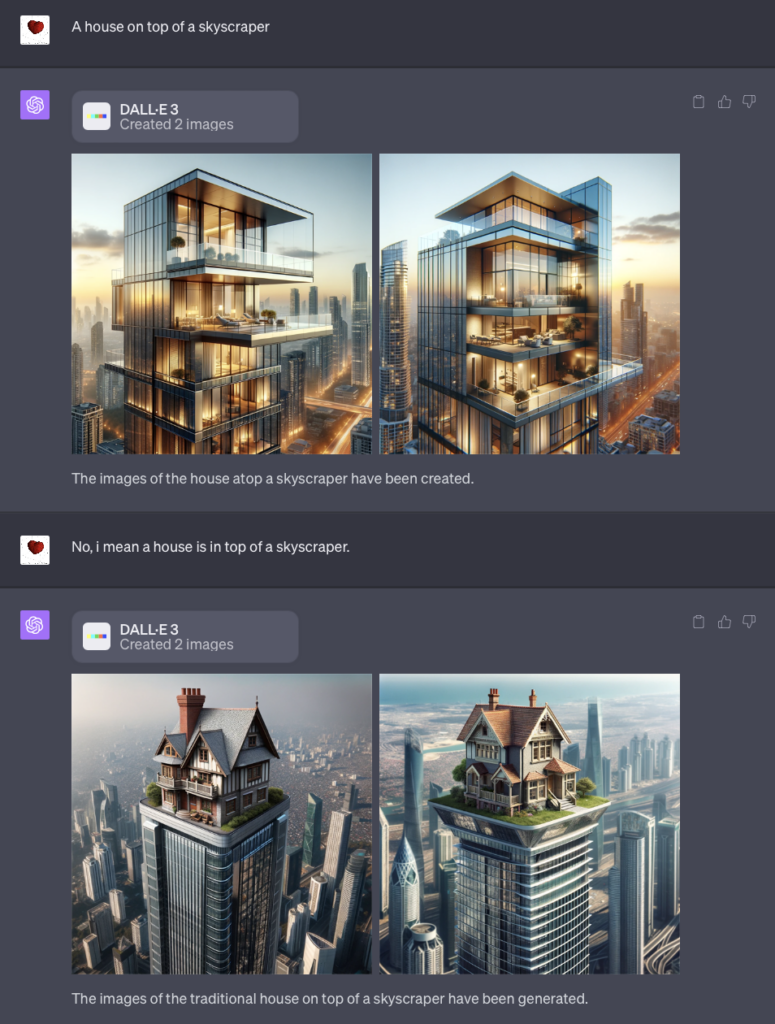
我强调了一下两个物体的位置关系，它果然就画对了。（离谱，我截图的时候才发现手抖把 on top 打成了 in top 这居然也画对了。）

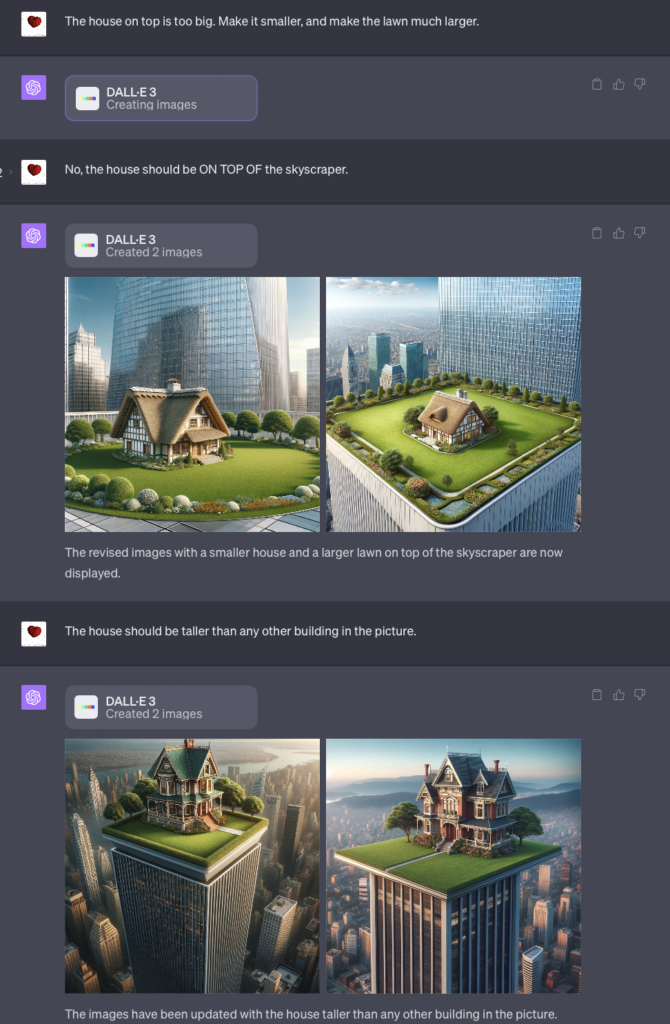
如果画的不好，还不满足心中的设想，可以给它提各种要求去修改。

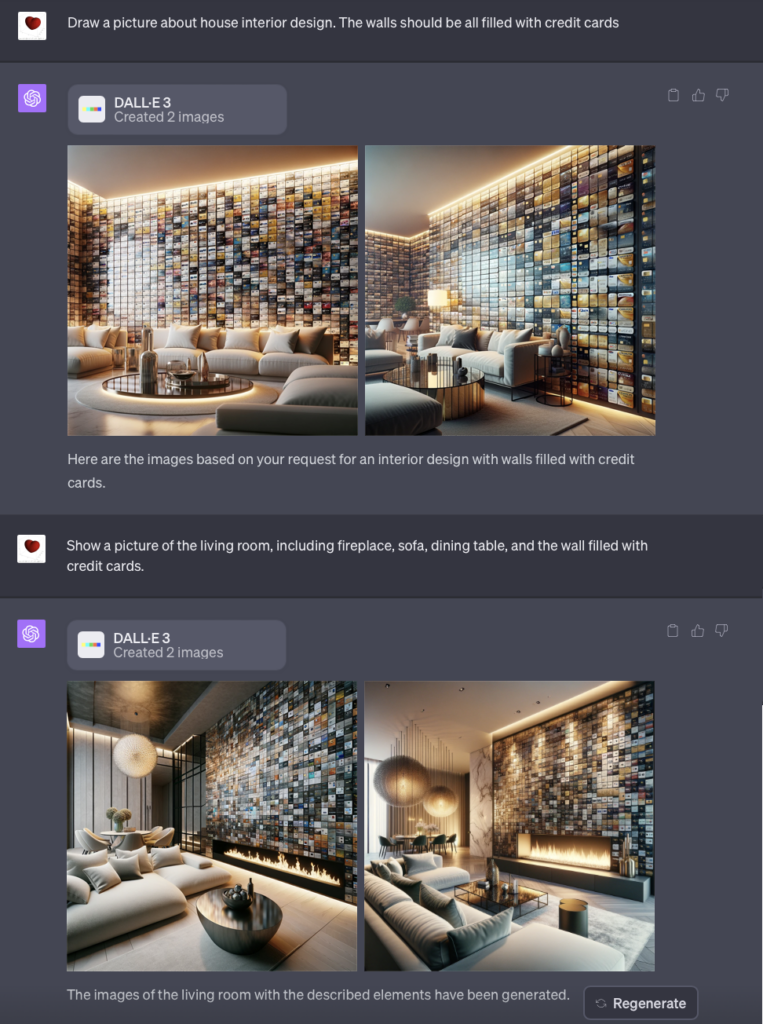
它可以画出我脑中设想的、现实世界中从未出现过的样子。

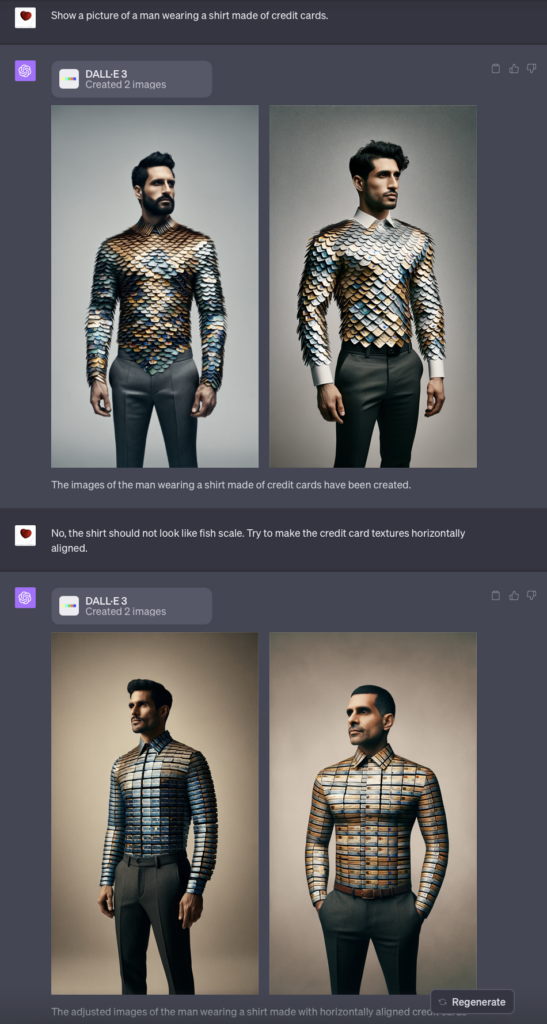
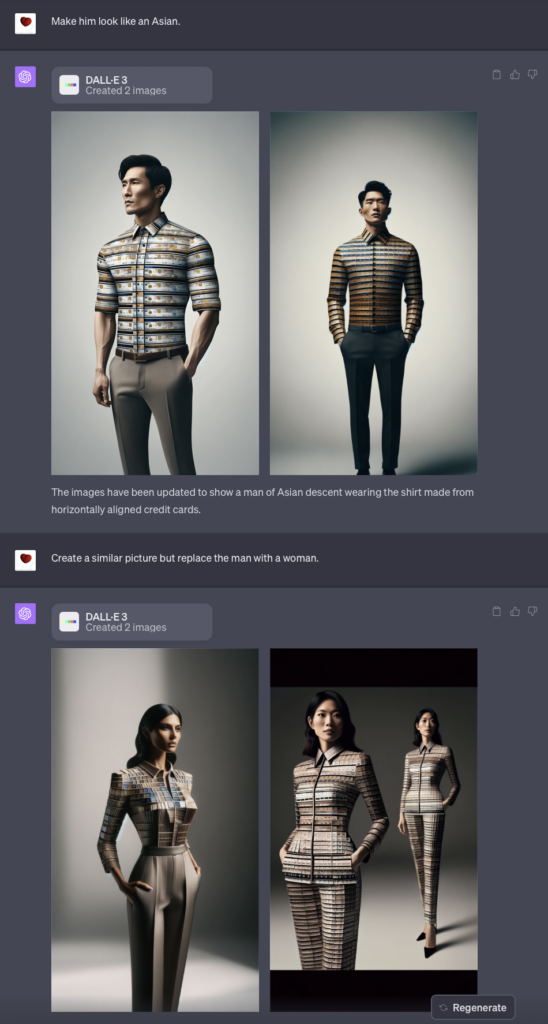
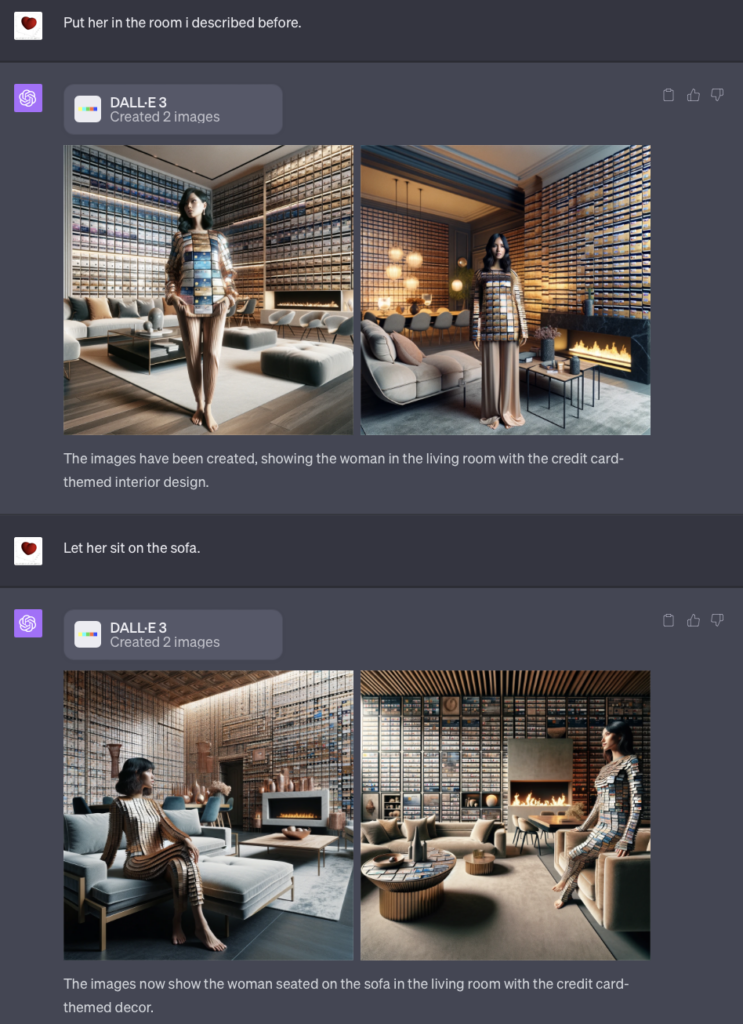
各种各样的修改意见都实现的挺好。

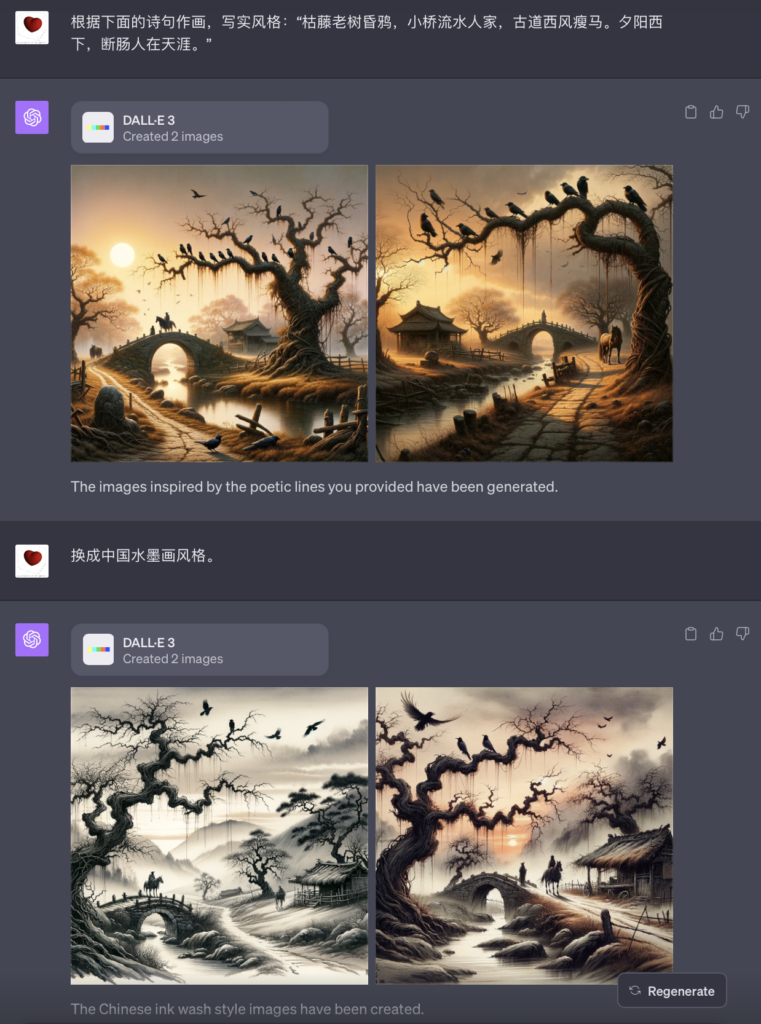
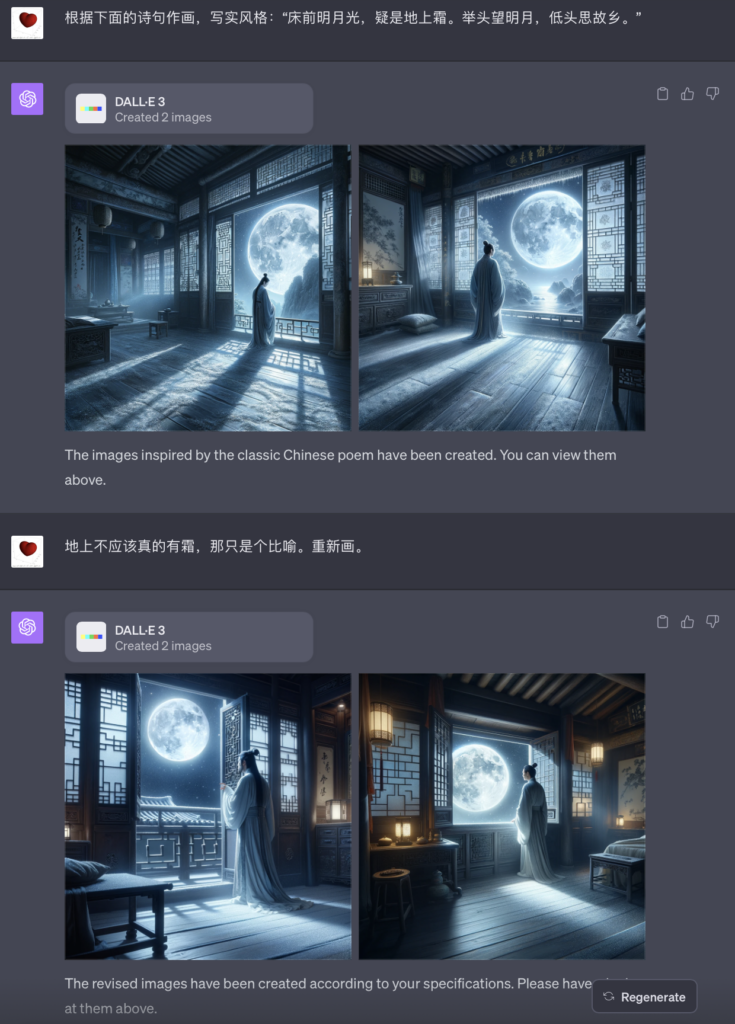
对中文的支持居然也很不错。

我个人感觉现在的AI画图水平，已经算是能提供生产力了，这个水平足矣应付很多要求不高的文章插图类的工作了。

有一个段子说得好：我们过去想象人工智能是，我们写诗画画编音乐，AI烧饭洗碗修电脑；没想到，现在是AI写诗画画编音乐，我们自己烧饭洗碗修电脑。…

闲聊一下爆火的ChatGPT：他能做什么、不能做什么

最近几年AI的进展十分迅猛，其中令人印象深刻的包括但不限于：基于 Diffusion Model 的各种图像生成模型、以及我今天想讨论的大语言模型 ChatGPT。尽管网上关于 ChatGPT 的讨论已经很多了，但是这东西确实足够有趣，因此我也来瞎扯几句吧。Disclaimer: 我是纯外行，对AI了解大概不比其他学物理的学生更多。

第一次使用 ChatGPT 的时候，有点让我回忆起了当年第一次见到 Google 时的场景。不过差距还是存在的，当我第一次使用 Google 时，我当即就知道这东西我会一辈子不停地使用它了；而 ChatGPT 大概还稍逊风骚，我目前并不觉得它能取代搜索引擎，它只适合完成一部分任务，而对另一部分任务则满嘴胡话无法信任其结果。

ChatGPT 既不像有些人以为的几乎成为通用人工智能了，也不像有些人以为的那样只是个玩具。我认为它的确可以在一些任务上潜在的提升生产力。这篇文章主要是探索一下 ChatGPT 能做什么、不能做什么。

✅ 能用来改进文档和Paper的语言

在美卡论坛的这个帖子里，大家在讲自己有哪些工作或生活中的实际需求已经被 ChatGPT 满足了的时候，提到最多的就是润色自己写的文档和paper的语言。甚至可以直接让 ChatGPT 给自己的paper写摘要。ChatGPT 的确在这方面至少比一个非英语母语的人好得多。

✅ 能用来应付Bullshit文章

也有很多人已经开始拿 ChatGPT 写那种根本没人看的诸如 year end review 之类的bullshit文章了。如果在我当年上学的时候就有 …

几个长见识的话题

最近大概是在这里写文比较少了，经常见到有人催更😂。在《我的人生追求》中我写道，“我的人生追求，就是：学习、分享，尽力给中文互联网贡献高质量内容。” 然而实际上值得分享的 non-trivial 的东西并不是很常见的，这也是本博客发文越来越少的主要原因。不过幸运的是，我参与创建的美卡论坛里面大神众多，里面有一些非常有趣的令人长见识的话题。这里就列一下过去一年中我觉得很涨姿势的几个话题吧，大家感兴趣的话可以移步那边继续阅读和参与讨论：

1. OverEmployed (OE)

自从疫情以后 Work From Home (WFH) 在美国变得非常普遍。这就给一个以前我想都没想过的神奇操作打开了大门：同时给多家公司全职工作！这个行为叫做 OverEmployed (OE)。美卡论坛中的相关帖子如下：

• 一个码农同时做5份工作，年入 $1.2M，每天还有4小时的游戏时间
• 最近消失了一段时间，现在给大家汇报一下目前OverEmployed(OE)的情况和进展

2. 润学（美国以外）

有些人是为了保留双国籍，有些人是为了给美国之外留个 plan B，总之美卡论坛里很多人开始对美国以外的移民身份感兴趣。可能不了解的人都会觉得奇怪，怎么一帮身在美国的人会对香港和墨西哥这种地方的身份有兴趣？Well，反正就是很多人有兴趣。美卡论坛中的相关帖子如下：

• 看大家疫情期间对香港很感兴趣，开个贴聊一下。
• 开个帖子记录反向润香港优才计划申请的status和timeline
• 香港12月28日新推出的高才通计划，3天批了。。。。
• 墨西哥永居/护照的获取难度
• 看了知乎这个帖子，貌似墨西哥绿卡可以花一点点钱随便办？
• 更多类似的话题可以移步美卡论坛-签证与身份（美国以外）

总之，美卡论坛是个好地方，大家有空多逛逛。…