西雅图地区拍摄 Mt Rainier 的地点推荐
作者: physixfanMt Rainier 是西雅图的著名景点之一。其实我们不必到它山脚下,在西雅图地区还有很多不错的角度可以拍摄它。我趁着西雅图今年最后的几个晴天(一说出来感觉好悲惨),找了几处好角度拍了点照片,抛砖引玉。
Kerry Park
 …
…
关于收入和财富不平等
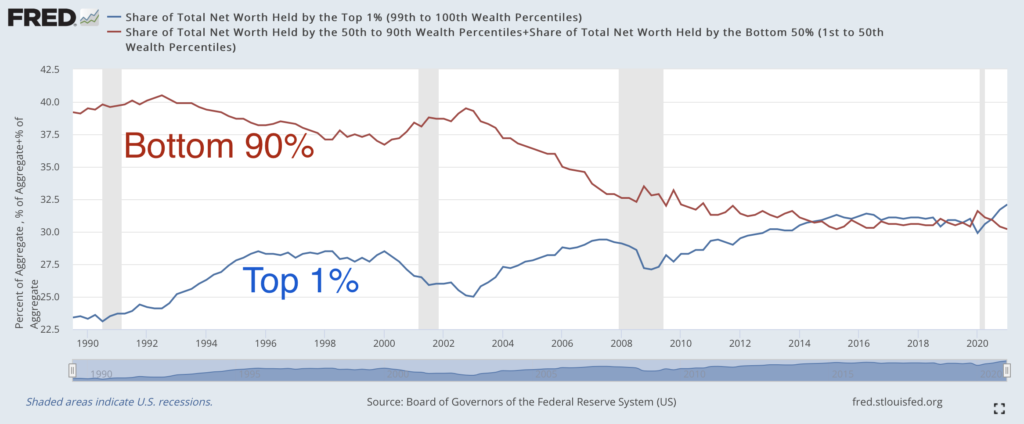
作者: physixfan【2021.8 更新】补充了2021Q1的 net worth top 1% vs bottom 90% 新数据。
wid.world 是个不错的网站,里面有很详细的各国收入不平等的数据。上图分别是美国的 top 0.1%, top 1%, bottom 50% 百分位收入的占比(截止到2019年)。可以很明显的看到,自从1980年左右开始,收入不平等就在一路狂飙:收入高的人的收入占比在持续升高,收入低的人的收入占比在持续下降。现在的不平等程度已经差不多回到了1930年代的水平了。
中国的数据在 wid.world 里其实也有,只不过我感觉不是很准确所以这里就不贴图了。其结果也是相似的,自从改革开放以来,收入不平等就在持续扩大,趋势和美国是类似的。
当然,也有收入不平等在缩小或维持不变的国家,比如欧洲各国。不过很不幸,当今世界发展最快的两个国家中国和美国都是收入不平等程度很高且还在持续扩大的;收入不平等程度低的国家例如欧洲各国都是经济发展某种程度上陷入了停滞的国家。
FRED 还有美国 net worth 占比的数据。上图蓝线是 top 1%、红线是 bottom 90% net worth 的占比(截止到2021Q1)。可以看到从有数据的1989年起,top 1% 的占比在随着时间推移不断扩大,近五年已经和整个 …
最好的科技股ETF是哪支?
作者: physixfanQQQ
当然,人人都知道科技股ETF的代表:纳指100ETF – QQQ。QQQ在过去20年稳稳的beat了SP500,几乎成了投资者的最爱。不过我个人对QQQ还是有些不满的:这个ETF的编制逻辑有点怪。一个公司在纳斯达克上市就优于在纽交所上市了?这显然没什么道理。我认为QQQ之所以能outperform SP500,最主要的原因应该还是因为它现在基本成了一支科技股基金。但纽交所里面也有些好的科技股,这些股票仅仅因为没有在纳斯达克上市,就被QQQ排除在外了。这类股票的例子包括但不限于:TWTR, SNAP, CRM, SQ, V, MA, 等等等等。这编制逻辑这么怪的话,如何令人信服它不会错过好股、可以继续一路高歌猛进呢?
所以我在想,如果想投资科技板块,有没有比QQQ更好的选择?
VGT, XLK 等
这几支ETF也是长期表现非常强劲,然而它们的致命缺陷是:作为科技股基金,持仓居然没有包括 GOOG, FB 和 AMZN!其实这类“科技股”sector基金都有一模一样的缺陷:GOOG 和 FB 被归类为 Communication Services sector,而 AMZN 被归类为 Consumer Discretionary sector。在我看来这三家公司不被归类为科技股简直是愚蠢,不过好像美帝的通行的分类就是这么做的。
IGM
这支基金是 “iShares Expanded Tech Sector ETF”,和前面几家相比,多了个 expanded。看一下这支 ETF …
(FIRE之后)如何一辈子不交税:买借死三部曲
作者: physixfan注:本文原载于美卡论坛。本文仅适用于生活在美国的朋友,不适用于生活在中国的朋友。毕竟中国本来就没有资本利得税、没有遗产税、也没有房产税,是如假包换的资本天堂,根本不需要考虑本文介绍的技巧就已经没有相关的税需要交了。
在这个帖子里 @AlfredW 的一条回复相当精彩,我觉得非常值得单独开个帖子讲一下这个税务规划的技巧。这个技巧仅适用于 FIRE (Financial Independent and Retire Early) 之后的人,还在打工拿W-2的人当然是没有办法不交税的。英文原文在这里:
https://www.peoplestaxpage.org/buy-borrow-die
第一步:买。
这一步非常简单粗暴,把你的所有资金all in VOO即可。
第二步:借。
让我们假设你有 $10M,那么all in VOO之后,按 FIRE 社区通常的 safe withdraw rate 4% 的话,每年可以消费 $400k。考虑到后面要讲的借钱,有利息,我们就假设只能花 3% 即 $300k 吧。
把所有钱全都all in VOO了,需要花钱钱从哪儿来呢?…
如何评价央行官员称“人民币中长期将升值,国际化条件下央行将放弃汇率目标”?
作者: physixfan汇率方面我也不是专业人士 不过还是来试着发表一点自己粗浅的看法吧。
RMB和USD之间的汇率,以前一直是有央行出面稳定的(虽然大家都不承认汇率操控)。在正常情况下,汇率这东西,具体数字是多高并不要紧,要紧的就是稳定,毕竟做跨国生意的人谁也不想让汇率一会儿飙升百分之百一会贬值百分之九十对吧。这方面中国央行的工作做得还是相当到位的,RMB对USD的汇率稳定性和其他货币相比一直非常出色。
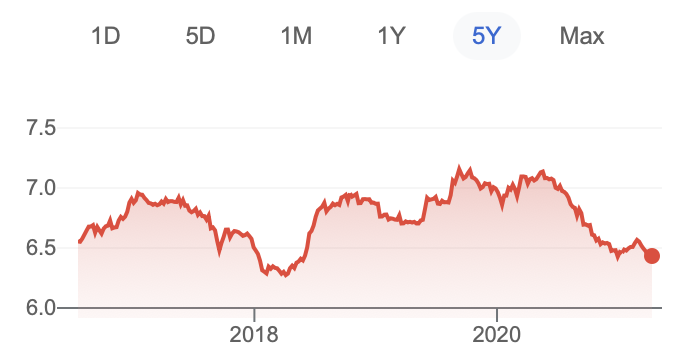
但是新冠疫情以来出现了特殊时期的特殊问题,那就是:美帝印钱速度实在是太快了… 下图是美国的M2五年来的变化,可以看到2020年3月以来印钱速度出现了前所未有的飙升,以至于当下M2总量的20%多都是2020年至今这一年半给印出来的:
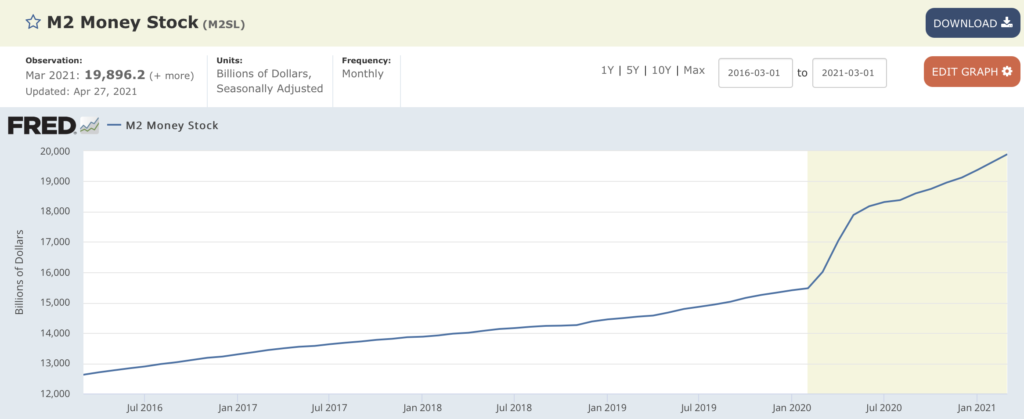
RMB-USD汇率稳定加上美帝疯狂印钱,这就导致了这么一个结果:美帝啥都不用干,仅仅凭借印钱,就可以大量购买中国生产的低价商品!新冠疫情以来,美帝人民躺在家里就已经收到了政府无差别发钱3次了,拿着这些凭空印出来的钱,就可以买到中国生产的物美价廉的商品… 凭啥?
所以在这样一个大环境下,我认为中国央行的汇率目标从稳定变成市场供需决定,是一个非常合理的举措。如果按照现在的市场供需,RMB 大概会升值一波的。
RMB 升值,当然有好处也有坏处。好处自然是全中国的人们都可以以更便宜的价格买到进口产品了,例如iPhone就会变便宜。另外中国一直需要从国外进口能源矿产之类的,在RMB升值之后也会变便宜。升值的主要坏处,是中国出口的商品价格竞争力会下降。不过在现在这个特殊时期,个人认为,即使中国出口的商品在国外涨价,依然不会对中国的出口竞争力构成太大的威胁,毕竟现在各大发展中国家基本上依然疫情肆虐,短时间内想找到中国的替代几乎是不可能的事儿。这大概正好是RMB升值的好时机吧。
有很多朋友搞混了一件事,就是RMB放开汇率波动,和RMB放开外汇管制,这是两回事。我知道很多人心里都觉得RMB应当贬值,因为国内房价太tm高了,卖一套北上深的房子,拿到上千万RMB,换成USD直接都可以去美国投资移民+财务自由了,如果RMB还能继续升值,这也太不可思议了。Well,这事儿确实很魔幻,所以我个人的判断是外汇管制绝对不会放开,至少在房价问题现状改变之前是不可能放开的。但汇率波动和外汇管制是两回事。
RMB如果真的会升值,这要如何指导投资呢?直接投资外汇期货风险太高,不建议普通人玩。如果你在中国、赚RMB、花RMB,那其实啥都不用做,尽情享受RMB升值之后购买进口产品的价格变便宜就好了。如果你在美国、赚USD、花USD,我个人的建议是,投资时除了美股美债美房,也要同时配置一定比例的中国股票,具体来说就是买中国沪深300基金ASHR+海外中概股基金MCHI,这样一来RMB升值的同时这些基金以USD计价也会跟着水涨船高。…
房贷利率对房价的影响
作者: physixfan我以前也没有认真关注过房贷利率对房价的影响,毕竟我自己做买房与否的决定时并没有参考当时利率有多高。不过随着我对房地产的认识越来越深入,现在明白了利率是房价驱动的主要因素之一。房贷利率降,则房价涨。
为什么利率对房价影响很大?
房贷利率降低1%,会导致月供减少多少?如果你没有用计算器算过,可能会被这个数字惊到。大家可以用这个网站算算看:
我们假设想买的房子房价是$1M,付20%的首付,贷30年固定利率贷款。那么:如果利率是4%(2020年及以前4%就已经很低了),则月供是 $3,819.32;如果利率是3%(2020年下半年开始就开始能拿到这么低的利率了),则月供是 $3,372.83。在这个例子中,利率降低了1%,直接导致月供降低了11.7%。从另一个角度来看也可以说,假设你只能付的出同样的月供,那你买房的购买力升高了13%。
即使你自己不会因为月供的问题升高买房预算,从社会整体来看,因为银行批贷款时决定贷款金额上限的主要依据就是 debt to income ratio 不能超过45%(如果你没有其他债务那么debt这一项就是你的买房月供),所以在income不变的情况下,若很多人选择根据银行批贷款的上限来撑预算,那么房价就是会涨那么多。
历史数据印证
下图是美国nominal房价(nominal意思是未经通胀调整的绝对金额)的历史走势图:
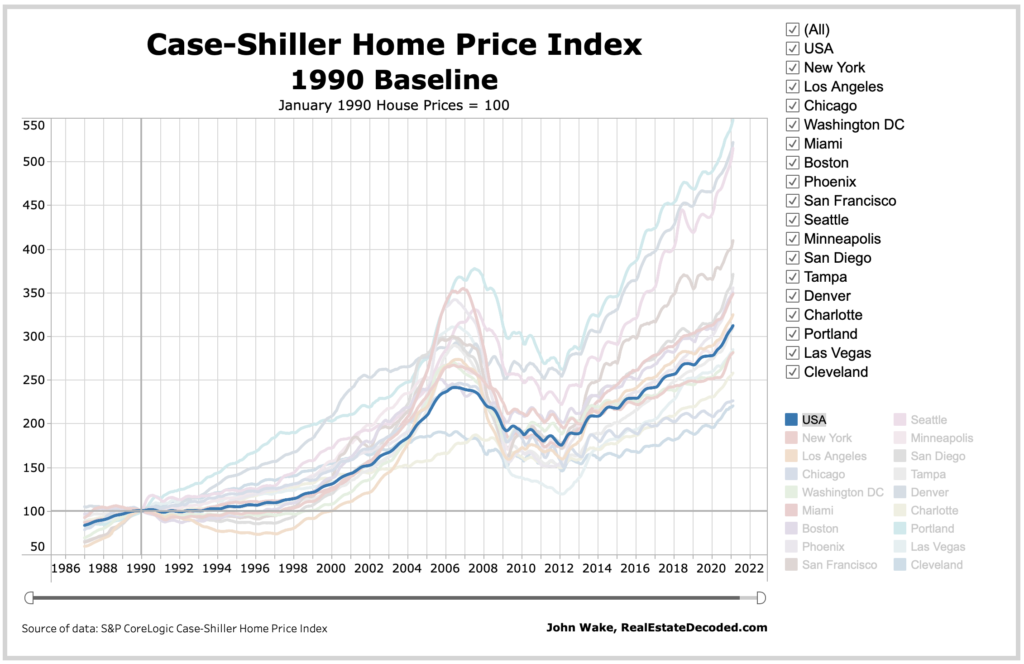
影响房价最大的两个因素是通胀和房贷利率。我们一一来看看影响有多大。
下图是美国通胀率的历史趋势图:
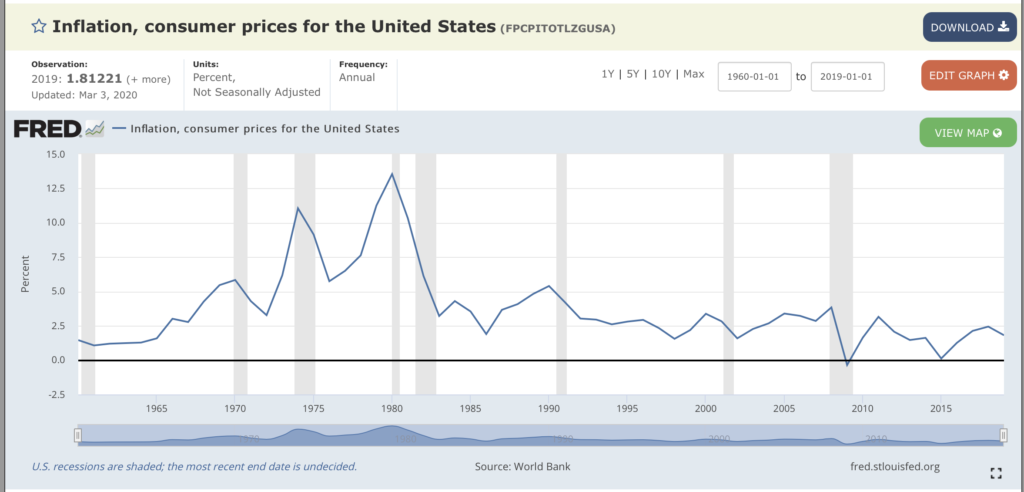
下图是美国real房价(real意思是经过通胀调整后的金额)的历史走势图:
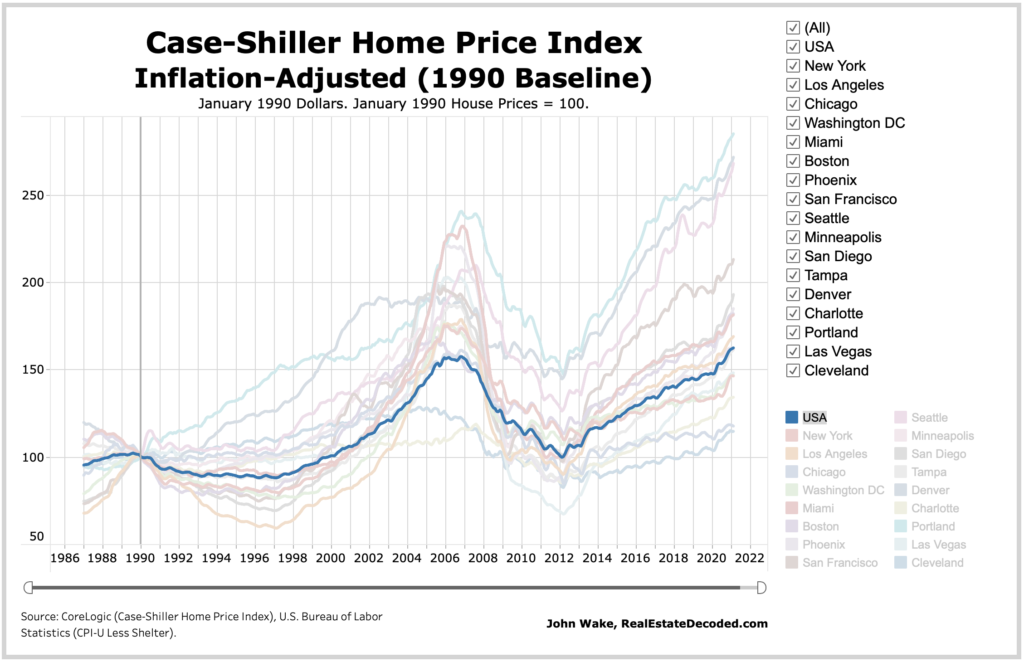
然后下图是房贷利率的历史走势图:
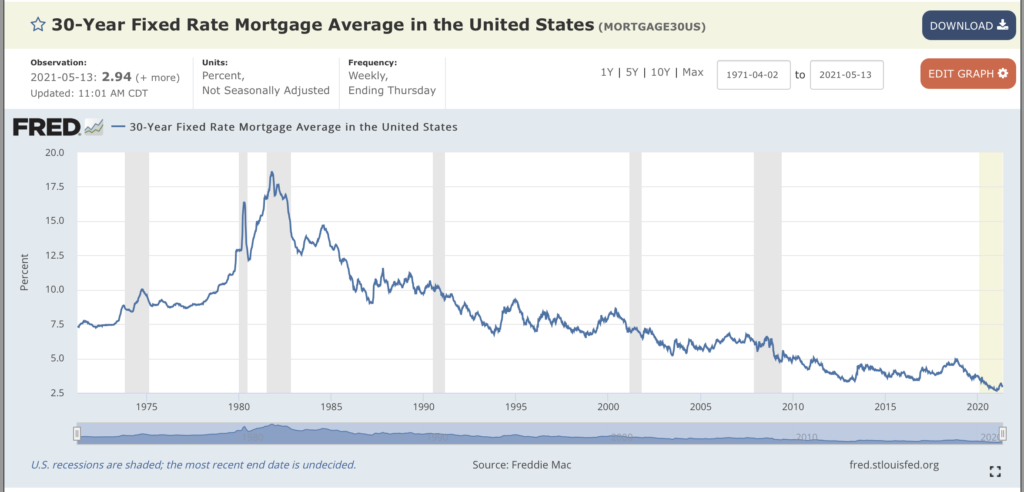
下图是美国real房价再经过利率调整之后的历史走势图:
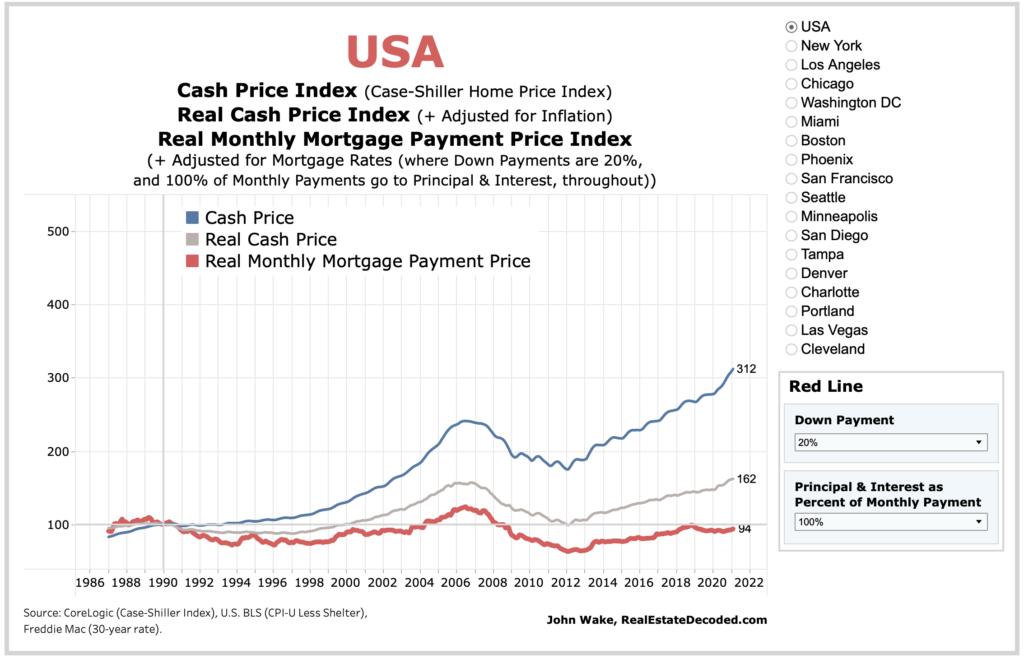
这张图如此令人震惊, 因为房价虽然nominal金额看起来一直在涨(除了2008年的次贷危机时期),但是经过通胀和房贷利率两个因素调整之后,整个曲线就被调整成了几乎是一条平线。也就是说美国平均房价几乎可以被通胀和房贷利率这俩因素解释个百分之八九十!
感谢 Real Estate Decoded 制作的精美图表!里面的图表还可以动态变化,可以自己选择感兴趣的城市查看。…