论邓文迪的战斗力
今天,一个隐藏多年的武林高手——一直备受争议的邓文迪终于向世人展现出了其惊人的武学修为。北京时间今日凌晨,在传媒大亨默多克就其旗下公司窃听丑闻举行的听证会上,一不明身份的愤青拿着一盘剃须膏冲到默多克面前,意欲袭击老人家。就在该男子将要得手之际,一直默默坐在丈夫身后的邓文迪瞬间爆发,在所有人都尚未反应过来之时,已然施展绝世神功,一招不太规范的“排山倒海”把歹徒拍翻在地!
如此敏捷的反应和迅速的出手实在令人称奇,下面死理性派就来具体估算一下邓文迪女士的出掌速度及打击威力。
出手速度
第一种方法,首先下载该视频之后逐帧播放,反复观察。下图是出手瞬间连续的3帧图像(很明显,除了武林高手邓文迪,其他人在如此短暂的时间里根本没有任何动作变化!)。该视频连续播放15帧之后,进度条上秒数增加1,这说明每两帧之间的时间间隔为1/15秒。因此下图的3帧之间经历的时间是2/15秒。

常在雨中跑,如何淋最少
相信大家经常会遇到这样一种囧况:在教室上了一天课,终于熬到可以回宿舍了,结果出门发现下起了大雨,而这时你既没有带伞又没有ggmm替你撑伞,在这样的情况下如何才能使自己淋到的雨量最少呢?
有一种很自然的想法,那就是尽可能快的跑回宿舍。但是这样也不见得是最好的,因为在你拼命往前跑的时候,有很多本来落不到你身上的雨滴会被你迎面撞上。那么究竟怎样才能淋雨最少呢?奔跑速度和身体倾斜角度是两个最关键因素。
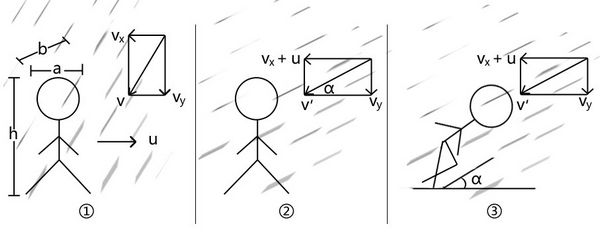
为了简化计算,我们近似的认为人体是个长方体,长 a 宽 b 高 h。假设雨滴匀速下落,水平速度 vx(vx可正可负),竖直速度 vy。设跑步速度为 u(如图1)。在地面上看,雨滴也在动,人也在动,看起来并不直观,于是我们切换到人参考系。在人参考系中,人是静止的,而雨滴的速度变为:竖直方向 vy,水平方向 vx(如图2)。如此一来,人应该以怎样的角度跑就显而易见了:在人参考系内,尽量让自己的身体和雨下落方向保持平行就可以了(如图3)。因为这样的角度可以保证只有头顶受雨淋,身体的其他侧面不会迎面撞上雨以及被雨打上。
容易算出身体的倾角 α = arctan [ vy / (vx+u) ]。
接下面来就要确定最优速度。…
什么是直线?
什么是直线?或者更加准确的问法是如何定义直线?不知道你有没有思考过这个问题。尽管我们实际生活中都有对直线概念的直观理解,但是考虑到后来非欧几何的问世,我们理应对直线有一个更深刻的认识。
欧几里得的几何原本上是这么定义直线的:“直线是它上面的点一样地平放着的线”,其中线的定义是“线只有长度而没有宽度”。显然在逻辑上这样的定义是极其不严格的,因为什么叫做“一样的平放着”只是一个日常生活中的直观概念。这也就是说欧几里得的几何原本相当于并没有对直线给出定义,尽管直线是几何学最基本的基本概念之一。
可能很多人会认为直线被定义成“两点间最短的线”(在这里就不去区分线段和直线了),然后就觉得在逻辑上就已经定义清楚了。但是这里还有一个问题,那就是什么叫做短?要有长短的概念就要先有距离的概念,而仅仅在几何学内考虑这个问题的话,要丈量距离就必须先有尺,而尺的形状又是直的,因此距离的概念其实是建立在直线的概念之上的。所以如果只考虑几何学那么用距离定义直线就成了循环定义了。
所以在数学上,我们就不能单从几何的角度去定义距离了。为了定义距离,我们需要在空间的每一个无穷小的区域上建立一个笛卡尔坐标系,在每一个小的笛卡尔坐标系内部可以通过普通的解析几何的方法定义出距离,然后在整个路径上对每一个小段上的距离进行叠加,从而定义出两点间连线的距离。之所以能在无穷小区域上建立笛卡尔坐标系,是因为一条曲线在无穷小区域上,我们可以把它近似为一小段直线(这个直线就是我们通常直观认识的直线),这个思想其实在最基础的微积分里面就已经有了。(如果一个空间奇异到在无穷小区域上无法建立笛卡尔坐标系,那么一般我们就不去研究它了。)至于为什么不能直接在大区域上直接建立笛卡尔坐标系来定义距离,原因很简单,坐标轴要画成直线啊,在没有直线概念的时候又哪里来的坐标轴呢…一个能够帮助理解的简单例子是在球面上定义最短线,如果直接建立笛卡尔坐标,其中的坐标轴就用我们直观感受的那种直线的话,那么最短线是必须脱离球面而经过球面之外的空间的。但是在球的表面的每一个无穷小区域上建立微小笛卡尔坐标系,就可以很好的沿着球表面定义出一条最短线。
至此,我们基本上可以把直线就定义成两点间距离最短的线了。但是,一定要知道一点,如此定义并没有定义出唯一一种直线。显然在一个球面上定义出的最短线,在我们看来其实是圆弧;在马鞍面上画出的最短线,在我们看来也是弯弯曲曲的线…他们都属于非欧几何。庞加莱圆盘模型(参见这篇文章)就是非欧几何的一种,按照那里定义的距离,圆盘模型内的直线在我们看来就成了圆弧了。
那么怎么定义才能保证刚才定义出来的直线就是我们通常直观上的直线呢?其实很简单,只要再加上一个公理,即传说中的欧几里得第五公设就可以实现:同一平面内一条线段和另外两条线段相交,若在某一侧的两个内角的和小于两直角,则这两线段经充分延长后在这一侧相交。非欧几何正是做出了与第五公设相反的假设而得名的,给出不同的公理,就会得出各种各样的非欧几何。
至此,我们终于可以引入Hilbert大神对直线的理解了:…
生命与负熵
热力学第二定律说道:在孤立热力学系统中,系统的熵永不减少。熵是用来表征系统混乱程度的物理量,因此这条定律实际上是在说,孤立系统的混乱程度永远是在增加的。直到达到热平衡,系统的熵达到了极大值,系统状态将不再改变,归于沉寂。“落叶永离,覆水难收;欲死灰之复燃,艰乎其力;愿破镜之重圆,冀也无端;人生易老,返老还童只是幻想;生米煮成熟饭,无可挽回。”【1】无数自然现象,无不印证着熵增原理的正确性。
然而,生命现象却似乎是个例外。生命是一种总是维持低熵的奇迹。一个生命,在它活着的时候,总是保持着一种高度有序的状态,各个器官各个细胞的运作井井有条。它并不会立即达到一种类似热力学平衡的不再活动的状态,相反,生物能够主动“做某些事情”、运动以及不断与外界进行物质能量交换恰恰是生物区别于普通物体的一个重要因素。而一个生命一旦死去,就会很快被熵增原理的强大威力给收服,很快将趋于热平衡状态,变成一片死寂的一堆极其无序的物质。那么,究竟是什么原因使得生命看似违背了普适的熵增原理呢?
问题的根源就在于,热力学第二定律只是用于“孤立系统”,即与外界没有物质、能量交换的系统。而生命之所以能长时间维持自身处在低熵有序状态,其秘诀正是在于它与外界的物质能量交换,即新陈代谢。
我们要搞清楚的是,新陈代谢的目的本质并不是交换物质。构成我们身体的原子,无非就是碳氢氧氮磷硫,和外界的普通原子没有什么区别,仅仅交换原子并不能给生命带来直接好处。
更应该明确的是,新陈代谢的目的本质也不是交换能量。似乎很长一段时间里,人们一直把吃饭喝水看成是单纯的吸收能量,认为生命以能量为生,而且至今大部分没有学过物理学的人也是这么看待的,人们满足于这样一种简单的理解。但是,“其实这非常荒唐,因为一个成年有机体所含的能量跟所含的物质一样,都是固定不变的。既然体内一个卡路里跟体外一个卡路里的价值是一样的,那么,确实不能理解单纯的能量交换究竟有什么用处。”【2】
那么,新陈代谢的本质究竟是什么呢?到底是怎样一种物理过程使得生命得以维持低熵,避免死亡呢?…
谣言粉碎机:粉笔摔倒地上会摔成几段?
昨天晚上宿舍夜聊的时候,dcr神牛说起了这样一件事实:一个粉笔掉到地上,无论它是以怎样的初始状态开始运动的,最后掉到地上,只要它摔断了,就一定是断成3段(而不是2段或者别的几段)。。。我当时听了之后世界观就崩溃了,怎么会是这样呢?要是说摔成2段就罢了,还可以理解,这个3段是怎么出来的。。。后来我在人人网上发状态,好多同学跟帖说,他们的高中老师或者力学老师也讲过这样一个事实。。。我当时就在奇怪,为什么哥活了20+年了,这样一个简单而又有趣的事实我就从来没有注意到过呢。。。
鉴于没有学过材料力学之类的课程,理论分析可能会不给力,所以我决定先做实验验证一下这个事实,然后通过实验现象思考一下原因。(结果今天白天给忘了,到了晚上才想起来,于是实验材料就只能是cz神牛从教学楼带回来的10跟粉笔。。。)
今天的实验结果如下:
如果粉笔从刚刚能摔断的高度下落,那么粉笔其实是摔成2段的。。。两段并不一样长,短的那段大概只有粉笔原长的1/4左右。。。至此,我相信谣言已经破解了。。。囧。。。
接下来的实验,是从更高一点的高度让它下落,如果从站直并且手臂平伸的高度下落的话,粉笔确实会摔成3段。这大概就是这条流言的起源吧,认为人一般来说都是从自己比较舒服的姿势去扔粉笔,然后这个高度范围恰好是让它断成三段的情况。。。
然后再次提升高度,…
量子永生
MWI(Many World Interpretation)平行宇宙理论(或多宇宙理论)是一个非常有意思的理论,它的提出是为了解释哥本哈根学派所面临的困难。
在解释著名的薛定谔的猫时,哥本哈根学派认为在观测前,猫处于既死又活的状态,然而一旦观测,波函数就坍缩了,我们有50%的概率观察到它死了,50%的概率观测到它还活着,但是现实世界里猫只有死或者活之中的一种状态。但是这种解释有一个问题,就是观测到底是什么意思,观测者是什么,用仪器记录下来而我们人类不去看,波函数到底坍缩了没有,最终会把问题归结到意识上面,一个拥有意识的“观测者”成了宇宙中拥有使波函数探索的至高无上的权利,似乎与我们对世界的认识不符。。
于是,平行宇宙理论粉墨登场~!MWI解释说,每次实验都会同时产生一只活猫和一只死猫,只不过他们存在于两个平行宇宙中,一个宇宙中猫死了,而另一个宇宙中猫还活蹦乱跳!当一个量子过程发生后,不光是猫被卷入了叠加态,整个宇宙也被卷入了叠加态!不同的平行宇宙之间不能产生任何联系,而我们也只能按照一定概率观测到某一个平行宇宙,这就解释了薛定谔的猫实验。时至今日,平行宇宙理论的支持者势力已经仅次于哥本哈根解释了,它在物理学界已经可以算是一种被广泛接受的正规理论了。
如果我们接受平行宇宙理论,那么就会得到很多有意思的结果。
你在这个世界为你错误的选择而痛苦,而这正是身处另一个量子分支的你快乐的表现。而这并不是最让人欣慰的结果,根据平行宇宙理论,你甚至是永生的~!…


