哥德尔定理
作者: physixfan哥德尔定理是数理逻辑中的一个定理,1931年奥地利逻辑、数学家克尔特.哥德尔(Kurt Godel)发现并证明的,这个定理彻底粉碎了希尔伯特的形式主义理想。为理解这个定理及其意义,需要相当的数理逻辑和集合论知识。要把这些预备知识都在这里整理出来,工作太繁重了,这也就是我一直没敢动手写这篇东西的原因之一。这里仍然也不打算详细介绍这些东西,只是在必要的时候给些简单的说明,要想更深刻地理解,有兴趣的朋友可以自学相关课程。
哥德尔定理其实是两个定理,其中哥德尔第一不完备性定理是最重要、也是误解最多的,从这一定理的版本众多就可以看出。如:
“如果一个形式理论T足以容纳数论并且无矛盾,则T必定是不完备的。”
“任何一个相容的数学形式化理论中,只要它强到足以在其中定义自然数的概念,就可以在其中构造在体系中既不能证明也不能否证的命题。”
“任何一个足够强的一致公设系统,必定是不完备的”
第二不完备性定理是第一定理的一个推论:“任何相容的形式体系不能用于证明它本身的相容性”
如果没有相关的知识基础,要理解这个定理真的是比较难。至于证明就更不容易看懂了。我偷点懒,跳过这些直接介绍其意义吧。…
初等数学证明开普勒第二定律
作者: physixfan开普勒第二定律是这么说的:在相等的时间内,行星与恒星的连线扫过的面积相等。当我第一眼看到这条定律的时候,觉得非常神奇,而当我看到了这个定律的证明时,不禁更觉神奇了!下面我把从《物理定律的本性》上看到的关于这个定理的证明简要写下来供大家欣赏。
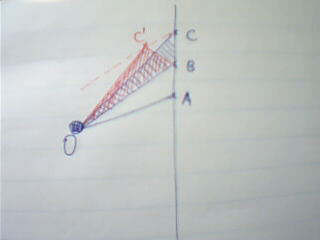
如图,O为恒星,直线AC为行星不受引力时的轨迹。设行星从A到B、从B到C所用的时间间隔Δt相等,A处的时刻为t1,B为t2,C为t3。现在假设行星不受O的引力作用,那么这时扫过的面积SΔABO和SΔBCO相等(等底同高)。现在行星受到引力作用了,因为引力的方向时刻指向恒星,所以在从t1到t3这段时间里,行星所受的引力的方向的总效果应该沿着BO方向(这需要一点向量的知识)。因此,t3时刻行星的位置C’应该由两个向量相加而得到:向量AC+向量CC’(作CC’平行于BO,因此沿BO方向的向量等价于CC’)。这样,SΔBCO=SΔBC’O(同底等高)。因此,SΔBC’O=SΔABO。因为Δt是任取的,所以在相等的时间内,行星与恒星的连线扫过的面积相等。
 …
…
奇妙的证明:周长相等的所有平面图形中,圆的面积最大
作者: physixfan我首先要证明,面积最大的图形满足一个性质:一条平分周长的直线(暂且把它叫做周长平分线),一定也平分面积。因为,如果不平分面积的话,那么我总可以把面积较大的那块翻到另一边去,使得周长不变,而面积增大(如左图,红色曲线围成的面积大于蓝色曲线)。好了,接下来,我要再证明面积最大的图形满足第二条性质:周长平分线与曲线的两个交点和曲线上任意一点构成的三角形,必然是直角三角形。因为,如果它不是直角三角形,我可以把他拉伸或压缩一下,使它成为直角三角形,这样新三角形的面积大于原三角形的面积(证明省略,主要使用S=absinθ/2),而图形其他部分面积不变,这样面积就扩大了。因此,面积最大的图形满足上述两条性质,我们就不难推出它是圆了。
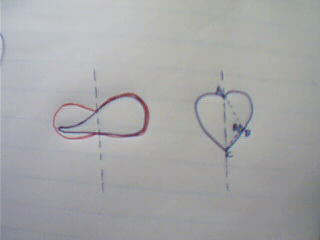 …
…
圈套
作者: physixfan最近佘飞告诉了我一个赌博的方法,乍一听真得挺管用,当时就在我们班掀起了一个热潮。
其方法大致是这样的:完诸如赌大小的几率对等的游戏时,假设你的本金足够大。第一次先压$1,如果输了,下次再压$2,如果这次又输了,下次压$4,如果还输,下次就压$8……一旦你赢了一次,先前所有的损失就全赢回来了,还赚$1,这时你再从$1压起。如此下来,你只要不连续输十几次,你就永远不会血本无归,总是一直一美元一美元的赚,赚到你满足为止。如果你连续输个十几次,那只能怨你运气实在太差了。
这么一听,还真有道理,如果真这么去赌,那不是只赚不赔么?
我有点怀疑,但不敢确定,于是第二天用电脑编了个程序来验证。源代码我懒得在敲一遍了,反正很简单,就是按这个方法模拟,用个随机函数来验证就行了。
结果出乎意料,当本金是$10000时,电脑刚运行了几十秒钟就显示本钱花光了。我又试了几次,结果还是如此。我又改了$100000,结果运行了几分钟都花光了本钱。难道这个方法行不通么?
后来,佘飞道出了其中的破绽。…
A Funny Mistake
作者: physixfanAt noon that day, we found a strange phenomenon. She Fei’s bottle, which was half filled with boiled water, had many bubbles going up from the bottom to the top, with the sound of ‘zizizizi’. It’s so interesting that Zhang …
找棒状物重心的简单办法
作者: physixfan分别用两手的食指支持住棒的两端,之后两手同时用力渐渐向中间并拢。这时,你会惊奇的发现,在任意时刻,只有一根手指头相对于棒在滑动,而另一只手指则会相对静止,尽管两只手都在用力。最终,两手靠在一起,这个地方一定就是棒的重心。其道理,主要是静摩擦力以及转轴平衡的知识。…


