…
…
…
…12
Aug
一只眼真的不能判断距离
作者： physixfan以前从很多书上看到这个结论，可我始终不能相信。我用一只眼，明明看到远的就是远，近的就是近，怎么会判断不了距离呢？
在浙大听讲几何光学的老师讲的一个实验之后，我是真的折服了。这个试验是这样的：闭上一只眼睛，伸出双手的食指，前后错开一定位置，然后尝试着把两指的指尖对到一起。你会惊奇的发现，这个事情你很难办到！可能会成功几次，但是并不是那么容易。如果你睁着两只眼试试，保准你不费吹灰之力就能办到！有意思！…
11
Aug
高考物理教育的失败——一个经典模型之错误
作者： physixfan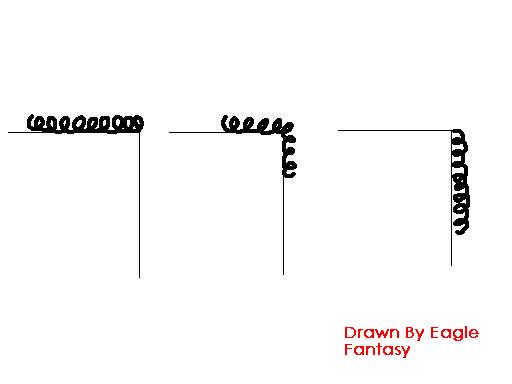
想必学过机械能守恒的高中生都作过这么一类题吧，如图，一个铁链原来静止的放在水平面上，漏出一点点可忽略不计，然后他会在重力作用下下滑，告诉你铁链的质量、长度一类东西，问你完全离开平面式铁链的速度（图中第三个状态）。
我当时也作过这一类题，《中学第二教材》把它当作一个重要专题来讲，训练机械能守恒。甚至在程稼夫《力学篇》上，都有一道类似的题，只不过麻烦一点就是了。
浙大讲动量能量的老师出出来这道题之后，我都很惊，这么简单的题，做个包子？一个机械能守恒不就完事了么。令我没有想到的是，经老师一点破，发现这道题是倒错题，所有这种类型的题全错了！…
