用逻辑学规范物理学(一)
最近因为看的物理方面的书比较多,就越来越感到有一些事情是不好的。我觉得现行的中学物理教材行文大约是按照当年物理学的发展史来的,而不是严谨的由公理推定理,通过严格的假设、推理、演绎以及归纳导出整个物理学。而且,至今我看过的所有读物都没有这样一个严谨的过程。现在,我们学生甚至得不到像质量、力这样的概念的准确定义,实在是可悲!(课本上说质量是物体所含物质的多少,纯粹就是种糊弄,根本不是定义,也不是质量的本质属性;说力是物体对物体的互相作用,这也只是一个诠释而非标准定义。)因此,我觉得我应该自己尝试着把牛顿力学通过这样一种方式使其严谨起来。而最近看的《科学与假设》(彭加勒著),更加使我坚定了这个信念。我不求得到世人的认可,只求自己看起来舒服。为此这几天我把逻辑学的一些东西自己看了看,觉得确实大有收获。今天我先把逻辑学的一些术语写一下吧,算是我的读书笔记。。。
1.属性与概念
属性:事物的性质与关系。
本质属性:事物独有的、区别于其他事物的属性。
概念:反映事物本质属性的思维形式。
概念的内涵:概念所反映的事物的本质属性。
概念的外延:具有这些属性的所有事物的集合。
2.概念的定义
定义分为属加种差的定义&发生式定义。
属概念与种概念:一个概念的外延是另一个概念的外延的真子集,则外延大的那个概念叫做属概念,外延小的那个概念叫做种概念。…
哥德尔定理
哥德尔定理是数理逻辑中的一个定理,1931年奥地利逻辑、数学家克尔特.哥德尔(Kurt Godel)发现并证明的,这个定理彻底粉碎了希尔伯特的形式主义理想。为理解这个定理及其意义,需要相当的数理逻辑和集合论知识。要把这些预备知识都在这里整理出来,工作太繁重了,这也就是我一直没敢动手写这篇东西的原因之一。这里仍然也不打算详细介绍这些东西,只是在必要的时候给些简单的说明,要想更深刻地理解,有兴趣的朋友可以自学相关课程。
哥德尔定理其实是两个定理,其中哥德尔第一不完备性定理是最重要、也是误解最多的,从这一定理的版本众多就可以看出。如:
“如果一个形式理论T足以容纳数论并且无矛盾,则T必定是不完备的。”
“任何一个相容的数学形式化理论中,只要它强到足以在其中定义自然数的概念,就可以在其中构造在体系中既不能证明也不能否证的命题。”
“任何一个足够强的一致公设系统,必定是不完备的”
第二不完备性定理是第一定理的一个推论:“任何相容的形式体系不能用于证明它本身的相容性”
如果没有相关的知识基础,要理解这个定理真的是比较难。至于证明就更不容易看懂了。我偷点懒,跳过这些直接介绍其意义吧。…
初等数学证明开普勒第二定律
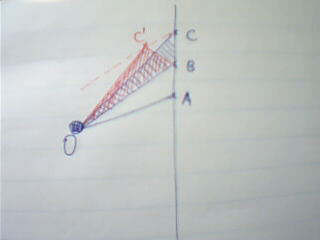
开普勒第二定律是这么说的:在相等的时间内,行星与恒星的连线扫过的面积相等。当我第一眼看到这条定律的时候,觉得非常神奇,而当我看到了这个定律的证明时,不禁更觉神奇了!下面我把从《物理定律的本性》上看到的关于这个定理的证明简要写下来供大家欣赏。
如图,O为恒星,直线AC为行星不受引力时的轨迹。设行星从A到B、从B到C所用的时间间隔Δt相等,A处的时刻为t1,B为t2,C为t3。现在假设行星不受O的引力作用,那么这时扫过的面积SΔABO和SΔBCO相等(等底同高)。现在行星受到引力作用了,因为引力的方向时刻指向恒星,所以在从t1到t3这段时间里,行星所受的引力的方向的总效果应该沿着BO方向(这需要一点向量的知识)。因此,t3时刻行星的位置C’应该由两个向量相加而得到:向量AC+向量CC’(作CC’平行于BO,因此沿BO方向的向量等价于CC’)。这样,SΔBCO=SΔBC’O(同底等高)。因此,SΔBC’O=SΔABO。因为Δt是任取的,所以在相等的时间内,行星与恒星的连线扫过的面积相等。
 …
…
奇妙的证明:周长相等的所有平面图形中,圆的面积最大
我首先要证明,面积最大的图形满足一个性质:一条平分周长的直线(暂且把它叫做周长平分线),一定也平分面积。因为,如果不平分面积的话,那么我总可以把面积较大的那块翻到另一边去,使得周长不变,而面积增大(如左图,红色曲线围成的面积大于蓝色曲线)。好了,接下来,我要再证明面积最大的图形满足第二条性质:周长平分线与曲线的两个交点和曲线上任意一点构成的三角形,必然是直角三角形。因为,如果它不是直角三角形,我可以把他拉伸或压缩一下,使它成为直角三角形,这样新三角形的面积大于原三角形的面积(证明省略,主要使用S=absinθ/2),而图形其他部分面积不变,这样面积就扩大了。因此,面积最大的图形满足上述两条性质,我们就不难推出它是圆了。
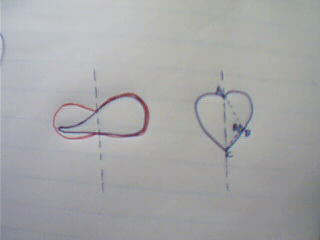 …
…


